
ස්කන්ධය $m$ වූ $P$ අංශුවක් හා ස්කන්ධය $\lambda m$ වූ $Q$ අංශුවක් පිළිවෙළින් $u$ හා $v$ වේගවලින් එකිනෙක දෙසට, සුමට තිරස් ගෙබිමක් මත වූ එක ම සරල රේඛාවක් දිගේ චලනය වේ. ඒවායේ ගැටුමෙන් පසු, $P$ අංශුව $v$ වේගයෙන් හා $Q$ අංශුව වේගයෙන් ප්රතිවිරුද්ධ දිශාවලට චලනය වේ. $\lambda=1$ බව පෙන්වා, $P$ හා $Q$ අතර ප්රත්යගති සංගුණකය සොයන්න.
කුඩා ඒකාකාර බෝලයක් රැගත් බැලුනයක් කාලය $t=0$ දී පොළොව මත ලක්ෂ්යයකින් නිශ්චලතාවයෙන් ආරම්භ කර ඒකාකාර $f$ ත්වරණයකින් සිරස් ව ඉහළට චලනය වේ; මෙහි $f$ වේ. කාලය $t=T$ හි දී බෝලය, බැලුනයෙන් සීරුවෙන් ඉවත් වී ගුරුත්වය යටතේ චලනය වේ. $t=0$ සිට බෝලය එහි උපරිම උස කරා ළඟා වන තෙක් බෝලයේ උඩු අත් චලිතය සඳහා ප්රවේග-කාල ප්රස්තාරයේ දළ සටහනක් අඳින්න. $T$, $f$ හා $g$ ඇසුරෙන්, බෝලය ළඟා වූ උපරිම උස සොයන්න.
රූපයේ $PABCD$ යනු තිරසට $30^0$ කින් ආනත අචල සුමට තලයක් මත තබා ඇති ස්කන්ධය $m$ වූ අංශුවකට ඈඳා ඇති සැහැල්ලු අවිතන්ය තන්තුවකි. තන්තුව, $A$ හි වූ අචල කුඩා සුමට කප්පියක් මතින් ද ස්කන්ධය $2m$ වූ සුමට කප්පියක් 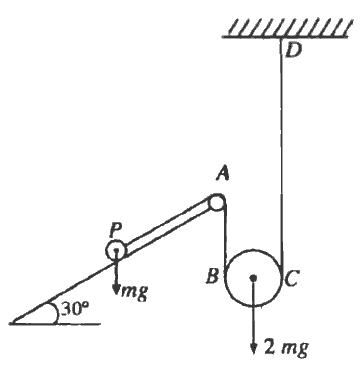 යටින් ද යයි. ලක්ෂ්යය අචල වේ. $PA$, උපරිම බෑවුම් රේඛාවක් දිගේ වන අතර $AB$ හා $CD$ සිරස් වේ. තන්තුව තදව ඇතිව පද්ධතිය නිශ්චලතාවයේ සිට මුදාහරිනු ලැබේ. අංශුවේ ත්වරණයෙහි විශාලත්වය සචල කප්පියේ ත්වරණයෙහි විශාලත්වය මෙන් දෙගුණයක් බව පෙන්වා, තන්තුවේ ආතතිය නිර්ණය කිරීමට ප්රමාණවත් සමීකරණ ලියා දක්වන්න.
යටින් ද යයි. ලක්ෂ්යය අචල වේ. $PA$, උපරිම බෑවුම් රේඛාවක් දිගේ වන අතර $AB$ හා $CD$ සිරස් වේ. තන්තුව තදව ඇතිව පද්ධතිය නිශ්චලතාවයේ සිට මුදාහරිනු ලැබේ. අංශුවේ ත්වරණයෙහි විශාලත්වය සචල කප්පියේ ත්වරණයෙහි විශාලත්වය මෙන් දෙගුණයක් බව පෙන්වා, තන්තුවේ ආතතිය නිර්ණය කිරීමට ප්රමාණවත් සමීකරණ ලියා දක්වන්න.
ස්කන්ධය $M kg$ වූ ට්රක් රථයක් ස්කන්ධය $m kg$ වූ කාරයක් ඍජු තිරස් පාරක් දිගේ ඇදගෙන යනු ලබන්නේ ට්රක් රථයේ හා කාරයේ චලිත දිශාවට සමාන්තර වූ සැහැල්ලු අවිතන්ය කේක්බලයක් ආධාරයෙනි. ට්රක් රථයේ හා කාරයේ චලිතයට ප්රතිරෝධ පිළිවෙළින් නිව්ටන් $\lambda M$ හා නිව්ටන් $\lambda m$ වේ; මෙහි $\lambda ( > 0)$ නියතයකි. එක්තරා මොහොතක දී ට්රක් රථයේ එන්ජිමෙන් ජනනය කරනු ලබන ජවය $PkW$ වන අතර ට්රක් රථයෙහි හා කාරයෙහි වේගය $v ms ^{-1}$ වේ. එම මොහොතේ දී කේබලයේ ආතතිය නිව්ටන් $\frac{1000mP}{(M + m)v}$ බව පෙන්වන්න.
සුපුරුදු අංකනයෙන්, $-\mathbf{i} + 2\mathbf{j}$ හා $2\alpha \mathbf{i} + \alpha \mathbf{j}$ යනු පිළිවෙළින් $O$ අචල මූලයකට අනුබද්ධයෙන් $A$ හා $B$ ලක්ෂ්ය දෙකක පිහිටුම් දෛශික යැයි ගනිමු; මෙහි $\alpha (>0)$ නියතයකි. අදිශ ගුණිතය භාවිතයෙන්, $A\hat{O}B = \frac{\pi}{2}$ බව පෙන්වන. $C$ යනු $OACB$ සෘජුකෝණාස්රයක් වන පරිදි වූ ලක්ෂ්යය යැයි ගනිමු. $\overrightarrow{OC}$ දෛශිකය $y-$අක්ෂය දිගේ පිහිටයි නම්, $\alpha$ හි අගය සොයන.
$OA$ හා $OB$ සැහැල්ලු අවිතන්ය තන්තු දෙකක් මගින් $O$ අචල ලක්ෂ්යයකින් එල්ලන ලද දිග $2\alpha$ හා බර $W$ වූ $AB$ ඒකාකාර දණ්ඩක් රූපයේ දැක්වෙන පරිදි සමතුලිතතාවයේ පවතී. $G$ යනු $AB$ හි මධ්ය ලක්ෂ්යය වේ. $A\hat{O}B = \frac{\pi }{2}$ හා 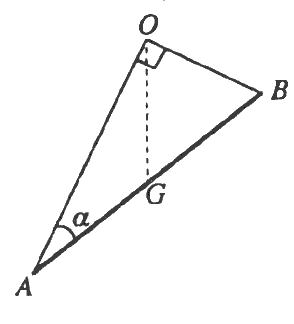 $O\hat{A}B = \alpha$ බව දී ඇත. $A\hat{O}G = \alpha$ බව පෙන්වා, තන්තු දෙකෙහි ආතති සොයන්න.
$O\hat{A}B = \alpha$ බව දී ඇත. $A\hat{O}G = \alpha$ බව පෙන්වා, තන්තු දෙකෙහි ආතති සොයන්න.
$A$ හා $B$ යනු $\Omega$ නියැදි අවකාශයක සිද්ධි දෙකක් යැයි ගනිමු. සුපුරුදු අංකනයෙන්, $P(A \cup B) = \frac{4}{5}$, $P(A' \cup B') = \frac{5}{6}$ හා $P(B | A) = \frac{1}{4}$ බව දී ඇත. $P(A)$ හා $P(B)$ සොයන්න.
මල්ලක, කාඩ් නවයක් අඩංගු වේ. ඒවායින් හතරක $1$ සංඛ්යාංකය මුද්රණය කර ඇති අතර ඉතිරි ඒවායේ $2$ සංඛ්යාංකය මුද්රණය කර ඇත. ප්රතිස්ථාපන රහිත ව වරකට එක බැගින් සසම්භාවීව මල්ලෙන් කාඩ් ඉවතට ගනු ලැබේ.
(i) ඉවතට ගත් පළමු කාඩ් දෙකෙහි සංඛ්යාංකයන්හි එකතුව හතර වීමේ,
(ii) ඉවතට ගත් පළමු කාඩ් තුනෙහි සංඛ්යාංකයන්හි එකතුව තුන වීමේ,
සම්භාවිතාව සොයන්න.
නිරීක්ෂණ හයක අගයන් $a, a, b, b, x$ හා $y$ වේ; මෙහි $a, b, x$ හා $y$ යනු ප්රභින්න ධන නිඛිල වන අතර $a වේ. මෙම නිරීක්ෂණ හයෙහි මාතයන් මොනවා ද?
මෙම මාතයන්හි ඓක්යය හා ගුණිතය පිළිවෙළින් $x$ හා $y$ බව දී ඇත. නිරීක්ෂණ හයෙහි මධ්යන $\frac{7}{2}$ නම්, $a$ හා $b$ සොයන්න.
$x_1, x_2, ... , x_{10}$ යන සංඛ්යා දහයෙහි මධ්යන්යය හා විචලතාව පිළිවෙළින් $10$ හා $9$ වේ. $x_{10}$ සංඛ්යාව ඉවත් කිරිමෙන් පසු ඉතිරි වන සංඛ්යා නවයෙහි ද මධ්යන්යය $10$ බව දී ඇත. මෙම සංඛ්යා නවයෙහි විචලතාව සොයන්න.
