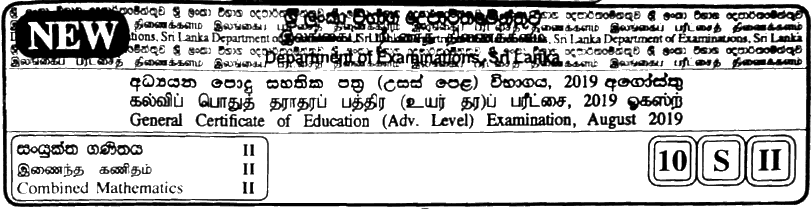
| (a) | P හා Q මෝටර් රථ දෙකක් සෘජු පාරක් දිගේ නියත ත්වරණ සහිතව එකම දිශාවකට චලනය වේ. කාලය t=0 හි දී P හි ප්රවේගය u ms−1 ද Q හි ප්රවේගය (u+9) ms−1 ද වේ. P හි නියත ත්වරණය f ms−2 ද Q හි නියත ත්වරණය (f+110) ms−2 ද වේ.
ප්රවේග-කාල වක්රවල දළ සටහන් අඳින්න. |
| (b) | සමාන්තර ඍජු ඉවුරු සහිත පළල a වූ ගගක් u ඒකාකාර ප්රවේගයෙන් ගලයි. රූපයෙහි, A,B,C හා D යන ඉවුරු මත වූ ලක්ෂ්ය සමචතුරස්රයක ශිර්ෂ වේ. ජලයට සාපේක්ෂව නියත v(>u) වේගයෙන් චලනය වන B1 හා B2 බෝට්ටු දෙකක් එකම මොහොතක A සිට ඒවායේ ගමන් ආරම්භ කරයි. B1 බෝට්ටුව පළමුව →AC දිගේ C වෙත ගොස් ඉන්පසු →CD දිශාවට ගග දිගේ ඉහළට D |
| (a) | රූපයෙහි ABC හා LMN ත්රිකෝණ, AˆCB=LˆNA=π4 හා AˆBC=LˆMN=π2 වූ BC හා MN අඩංගු මුහුණත් සුමට තිරස් ගෙබිමක් මත තබන ලද පිළිවෙළින් X හා Y සර්වසම සුමට ඒකාකාර කුඤ්ඤ දෙකක ගුරුත්ව කේන්ද්ර තුළින් වූ සිරස් හරස්කඩ වේ. |
| (b) | රූපයේ පෙන්වා ඇති පරිදි සුමට සිහින් ABCDE බටයක් සිරස් තලයක |
තිරසට π6 කෝණයකින් ආනත සුමට අචල තලයක උපරිම බෑවුම් රේඛාවක් 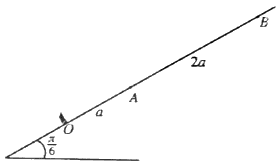 මත OA=a හා AB=2a වන පරිදි O පහළම ලක්ෂ්යය ලෙස ඇතිව O,A හා B ලක්ෂ්ය එම පිළිවෙළින් පිහිටා ඇත. ස්වාභාවික දිග a හා ප්රත්යස්ථතා මාපාංකය mg වූ සැහැල්ලු ප්රත්යාස්ථ තන්තුවක එක් කෙළවරක් O ලක්ෂයට ඇදා ඇති අතර අනෙක් කෙළවර ස්කන්ධය m වූ P අංශුවකට ඈඳා ඇත. P අංශුව B ලක්ෂ්යය කරා ළගා වන තෙක් තන්තුව OAB රේඛාව දිගේ අදිනු ලැබේ. ඉන්පසු P අංශුව නිශ්චලතාවයේ සිට මුදා හරිනු ලැබේ. B සිට A දක්වා P හි චලිත සමීකරණය, 0≤x≤2a සදහා, ¨x+ga(x+a2)=0 මගින් දෙනු ලබන බව පෙන්වන්න; මෙහි AP=x වේ.
මත OA=a හා AB=2a වන පරිදි O පහළම ලක්ෂ්යය ලෙස ඇතිව O,A හා B ලක්ෂ්ය එම පිළිවෙළින් පිහිටා ඇත. ස්වාභාවික දිග a හා ප්රත්යස්ථතා මාපාංකය mg වූ සැහැල්ලු ප්රත්යාස්ථ තන්තුවක එක් කෙළවරක් O ලක්ෂයට ඇදා ඇති අතර අනෙක් කෙළවර ස්කන්ධය m වූ P අංශුවකට ඈඳා ඇත. P අංශුව B ලක්ෂ්යය කරා ළගා වන තෙක් තන්තුව OAB රේඛාව දිගේ අදිනු ලැබේ. ඉන්පසු P අංශුව නිශ්චලතාවයේ සිට මුදා හරිනු ලැබේ. B සිට A දක්වා P හි චලිත සමීකරණය, 0≤x≤2a සදහා, ¨x+ga(x+a2)=0 මගින් දෙනු ලබන බව පෙන්වන්න; මෙහි AP=x වේ.
y=x+a2 යැයි ගෙන ඉහත චලිත සමීකරණය a2≤y≤5a2 සඳහා ¨y+ω2y=0 ආකාරයෙන් නැවත ලියන්න; මෙහි ω=√ga වේ.
ඉහත සරල අනුවර්තී චලිතයේ කේන්ද්රය සොයා ˙y2=ω2(c2−y2) සුත්රය භාවිතයෙන්, c විස්තාරය හා A වෙත ළගා වන විට P හි ප්රවේගය සොයන්න.
O වෙත ළගා වන විට P හි ප්රවේගය √7ga බව පෙන්වන්න.
B සිට O දක්වා චලනය වීමට P මගින් ගනු ලබන කාලය √ga{cos−1(15)+2k} බවත් පෙන්වන්න; මෙහි k=√7−√6 වේ.
P අංශුව O වෙත ළඟා වන විට, තලයට ලම්බව O හි සවිකර ඇති සුමට බාධකයක් හා එය ගැටෙයි. බාධකය හා P අතර ප්රත්යාගති සංගුණකය e වේ. 0<e≤1√7 නම්, පසුව සිදු වන P හි චලිතය සරල අනුවර්තී නොවන බව පෙන්වන්න.
| (a) | OACB යනු සමාන්තරාස්රයක් යැයි ද D යනු AC මත AD:DC=2:1 වන පරිදි වූ ලක්ෂ්යය යැයි ද ගනිමු. O අනුබද්ධයෙන් A හා B ලක්ෂ්යවල පිහිටුම් දෛශික පිළික්වෙළින් λ a හා b වේ: මෙහි λ>0 වේ. →OC හා →BD දෛශික, a,b හා λ ඇසුරෙන් ප්රකාශ කරන්න. | ||||||||||||
| (b) | කේන්ද්රය O හා පැත්තක දිග 2a වූ ABCDEF සවිධි ෂඩස්රයක තලයෙහි වූ බල තුනකින් පද්ධතියක් සමන්විත වේ. මූලය O හි ද Ox−අක්ෂය →OB දිගේ ද Oy−අක්ෂය →OH දිගේ ද ඇතිව බල හා ඒවායේ ක්රියා ලක්ෂ්ය, සුපුරුදු අංකනයෙන්, පහත වගුවේ දක්වා ඇත; මෙහි H යනු CD හි මධ්ය ලක්ෂ්යය වේ.
පද්ධතිය යුග්මයකට තුල්ය වන බව පෙන්වා, යුග්මයේ ඝූර්ණය සොයන්න. |
| (a) | එක එකක දිග 2a වූ AB හා BC |
| (b) | රූපයෙහි පෙන්වා ඇති රාමු සැකිල්ල ඒවායේ
සොයන්න. |
- (i) අරය a වූ තුනී ඒකාකාර අර්ධ වෘත්තාකාර කම්බියක ස්කන්ධ කේන්ද්රය එහි කේන්ද්රයේ සිට 2aπ දුරකින් ද
- (ii) අරය a වූ තුනී ඒකාකාර අර්ධ ගෝලාකාර කබොළක ස්කන්ධ කේන්ද්රය එහි කේන්ද්රයේ සිට a2 දුරකින් ද
පිහිටන බව පෙන්වන්න.
 කේන්ද්රය O හා අරය 2a වූ තුනී ඒකාකාර අර්ධ ගෝලාකාර කබොළකට රූපයේ දැක්වෙන පරිදි දිග 2πa වූ AB සෘජු කොටසකින් ද BD විෂ්කම්භය AB ට ලම්බ වන පරිදි, අරය a වූ BCD අර්ධ වෘත්තාකාර කොටසකින් ද සමන්විත ඒකාකාර කම්බියකින් සාදනු ලැබූ ABCD තුනී මිටක් දෘඪ ලෙස සවි කිරීමෙන් හැන්දක් සාදා ඇත. A ලක්ෂ්යය අර්ධ ගෝලයේ ගැට්ට මත ඇති අතර OA යන්න AB ට ලම්බ ද OD යන්න AB ට සමාන්තර ද වේ. තව ද BCD යන්න OABD හි තලයේ පිහිටා ඇත. අර්ධ ගෝලයේ ඒකක වර්ගඵලයක ස්කන්ධය σ ද මිටෙහි ඒකක දිගක ස්කන්ධය aσ2 ද වේ. හැන්දේ ස්කන්ධ කේන්ද්රය, OA සිට පහළට 219π(8π−2π2−1)a දුරකින් ද O හා D හරහා යන රේඛාවේ සිට 519a දුරකින් ද පිහිටන බව පෙන්වන්න.
කේන්ද්රය O හා අරය 2a වූ තුනී ඒකාකාර අර්ධ ගෝලාකාර කබොළකට රූපයේ දැක්වෙන පරිදි දිග 2πa වූ AB සෘජු කොටසකින් ද BD විෂ්කම්භය AB ට ලම්බ වන පරිදි, අරය a වූ BCD අර්ධ වෘත්තාකාර කොටසකින් ද සමන්විත ඒකාකාර කම්බියකින් සාදනු ලැබූ ABCD තුනී මිටක් දෘඪ ලෙස සවි කිරීමෙන් හැන්දක් සාදා ඇත. A ලක්ෂ්යය අර්ධ ගෝලයේ ගැට්ට මත ඇති අතර OA යන්න AB ට ලම්බ ද OD යන්න AB ට සමාන්තර ද වේ. තව ද BCD යන්න OABD හි තලයේ පිහිටා ඇත. අර්ධ ගෝලයේ ඒකක වර්ගඵලයක ස්කන්ධය σ ද මිටෙහි ඒකක දිගක ස්කන්ධය aσ2 ද වේ. හැන්දේ ස්කන්ධ කේන්ද්රය, OA සිට පහළට 219π(8π−2π2−1)a දුරකින් ද O හා D හරහා යන රේඛාවේ සිට 519a දුරකින් ද පිහිටන බව පෙන්වන්න.
රළු තිරස් මේසයක් මත, අර්ධ ගෝලාකාර පෘෂ්ඨය එය ස්පර්ශ කරමින්, හැන්ද තබා ඇත. අර්ධ ගෝලාකාර පෘෂ්ඨය හා මේසය අතර ඝර්ෂණ සංගුණකය 17 කි. →AO දිශාවට A හි දී යොදනු ලබන තිරස් බලයක් මගින් OD සිරස්ව ඇතිව හැන්ද සමතුලිතතාවයේ තැබිය හැකි බව පෙන්වන්න.
| (a) | ආරම්භයේ දී එක එකක් සුදු පාට හෝ කළු පාට වූ, පාටින් හැර අන් සෑම අයුරකින්ම සමාන බෝල 3 ක් පෙට්ටියක අඩංගු වේ. දැන්, පාටින් හැර අන් සෑම අයුරකින්ම පෙට්ටියේ ඇති බෝලවලට සමාන සුදු පාට බෝලයක් පෙට්ටිය තුළට දමා ඉන්පසු සසම්භාවී ලෙස බෝලයක් පෙට්ටියෙන් ඉවතට ගනු ලැබේ. පෙට්ටියේ ඇති බෝලවල ආරම්භක සංයුති හතර සම සේ භව්ය වේ යැයි උපකල්පනය කරමින්,
බෝල 2 ක් තිබීමේ, සම්භාවිතාව සොයන්න. | ||||||||||||
| (b) | μ හා σ යනු පිළිවෙළින් {xi:i=1,2,...,n} අගයන් කුලකයේ මධ්යන්යය හා සම්මත අපගමනය යැයි ගනිමු. {αxi:i=1,2,...,n} අගයන් කුලකයේ මධ්යන්යය හා සම්මත අපගමනය සොයන්න; මෙහි α යනු නියතයකි.
සේවකයින් 50 දෙනාගේ මාසික වැටුප්වල මධ්යන්යය හා සම්මත අපගමනය නිමානය කරන්න. |

 වෙත යයි.
වෙත යයි. 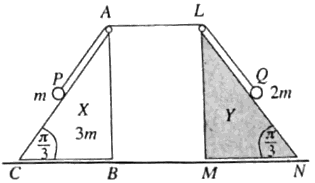 ස්කන්ධය
ස්කන්ධය 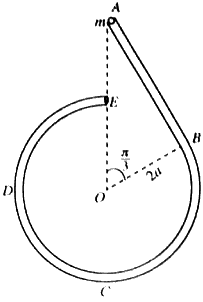 සවිකර ඇත. දිග
සවිකර ඇත. දිග  ඒකාකාර දඬු දෙකක්
ඒකාකාර දඬු දෙකක්  කෙළවරවල දී සුමට ලෙස සන්ධි කළ
කෙළවරවල දී සුමට ලෙස සන්ධි කළ