| (a) | රූපයෙහි ABC හා LMN ත්රිකෝණ, AˆCB=LˆNA=π4 හා AˆBC=LˆMN=π2 වූ BC හා MN අඩංගු මුහුණත් සුමට තිරස් ගෙබිමක් මත තබන ලද පිළිවෙළින් X හා Y සර්වසම සුමට ඒකාකාර කුඤ්ඤ දෙකක ගුරුත්ව කේන්ද්ර තුළින් වූ සිරස් හරස්කඩ වේ. 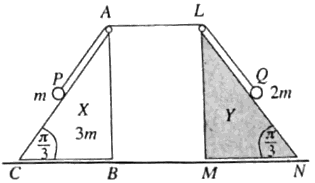 ස්කන්ධය 3m වූ X කුඤ්ඤය ගෙබිම මත චලනය වීමට නිදහස් වන අතර Y කුඤ්ඤය අචලව තබා ඇත. AC හා LN රේඛා අදාළ මුහුණත්වල උපරිම බෑවුම් රේඛා වේ. A හා L හි සවිකර ඇති සුමට කුඩා කප්පි දෙකක් මතින් යන සැහැල්ලු අවිතන්ය තන්තුවක දෙකෙළවර ස්කන්ධ පිළිවෙළින් m හා 2m වූ P හා Q අංශු දෙකකට ඈඳා ඇත. රූපයේ පරිදි ආරම්භක පිහිටීමේ දී, තන්තුව නොබුරුල්ව හා AP=AL=LQ=a වන ලෙස P හා Q අංශු පිළිවෙළින් AC හා LN මත අල්වා තබා ඇත. පද්ධතිය නිශ්චලතාවයෙන් මුදා හරිනු ලැබේ. Y වෙත යාමට X ගනු ලබන කාලය, a හා g ඇසුරෙන් නිර්ණය කිරීමට ප්රමාණවත් සමීකරණ ලබා ගන්න. ස්කන්ධය 3m වූ X කුඤ්ඤය ගෙබිම මත චලනය වීමට නිදහස් වන අතර Y කුඤ්ඤය අචලව තබා ඇත. AC හා LN රේඛා අදාළ මුහුණත්වල උපරිම බෑවුම් රේඛා වේ. A හා L හි සවිකර ඇති සුමට කුඩා කප්පි දෙකක් මතින් යන සැහැල්ලු අවිතන්ය තන්තුවක දෙකෙළවර ස්කන්ධ පිළිවෙළින් m හා 2m වූ P හා Q අංශු දෙකකට ඈඳා ඇත. රූපයේ පරිදි ආරම්භක පිහිටීමේ දී, තන්තුව නොබුරුල්ව හා AP=AL=LQ=a වන ලෙස P හා Q අංශු පිළිවෙළින් AC හා LN මත අල්වා තබා ඇත. පද්ධතිය නිශ්චලතාවයෙන් මුදා හරිනු ලැබේ. Y වෙත යාමට X ගනු ලබන කාලය, a හා g ඇසුරෙන් නිර්ණය කිරීමට ප්රමාණවත් සමීකරණ ලබා ගන්න. |
| (b) | රූපයේ පෙන්වා ඇති පරිදි සුමට සිහින් ABCDE බටයක් සිරස් තලයක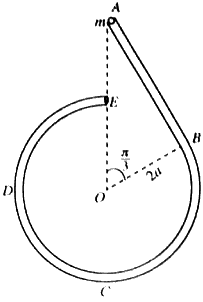 සවිකර ඇත. දිග 2√3a වූ AB කොටස ඍජු වන අතර එය B හි දී අරය 2a වූ BCDE වෘත්තාකාර කොටසට ස්පර්ශක වේ. A හා E අන්ත O කේන්ද්රයට සිරස්ව ඉහළින් පිහිටයි. ස්කන්ධය m වූ P අංශුවක් A හි දී බටය තුළ තබා නිශ්චලතාවයේ සිට සීරුවෙන් මුදා හරිනු ලැබේ. →OA සමග θ(π3<θ<2π) කෝණයක් →OP සාදන විට P අංශුවේ වේගය, v යන්න, v2=4ga(2−cosθ) මගින් දෙනු ලබන බව පෙන්වා, එම මොහොතේ දී P අංශුව මත බටයෙන් ඇති කරන ප්රතික්රියාව සොයන්න. සවිකර ඇත. දිග 2√3a වූ AB කොටස ඍජු වන අතර එය B හි දී අරය 2a වූ BCDE වෘත්තාකාර කොටසට ස්පර්ශක වේ. A හා E අන්ත O කේන්ද්රයට සිරස්ව ඉහළින් පිහිටයි. ස්කන්ධය m වූ P අංශුවක් A හි දී බටය තුළ තබා නිශ්චලතාවයේ සිට සීරුවෙන් මුදා හරිනු ලැබේ. →OA සමග θ(π3<θ<2π) කෝණයක් →OP සාදන විට P අංශුවේ වේගය, v යන්න, v2=4ga(2−cosθ) මගින් දෙනු ලබන බව පෙන්වා, එම මොහොතේ දී P අංශුව මත බටයෙන් ඇති කරන ප්රතික්රියාව සොයන්න.
P අංශුව A සිට B දක්වා චලිතයේ දී එය මත බටයෙන් ඇති කරන ප්රතික්රියාව ද සොයන්න.
P අංශුව B පසු කරන විට P අංශුව මත බටයෙන් ඇති කරන ප්රතික්රියාව ක්ෂණිකව වෙනස් වන බව පෙන්වන්න. |

 ස්කන්ධය
ස්කන්ධය  සවිකර ඇත. දිග
සවිකර ඇත. දිග