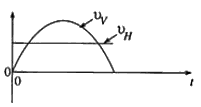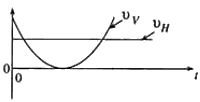ප්ලන්ක් නියතයේ SI ඒකකය වන්නේ
ගමන් කිරීම සඳහා භෞතික මාධ්‍යයක් අවශ්‍ය වන්නේ පහත කුමන තරංග වලට ද?
ප්‍රකාශ ඉලෙක්ට්‍රෝන විමෝචනය සඳහා දේහලී සංඛ්‍යාතය $f_0$ වන ප්‍රකාශ සංවේදී පෘෂ්ඨයක් මතට සංඛ්‍යාතය $f$ වන විද්‍යුත් චුම්බක විකිරණ පතිත වේ.
පහත දක්වා ඇති කුමක් අසත්‍ය වේ ද?
ධ්වනියේ වේගය පිළිබඳව කර ඇති පහත සඳහන් ප්‍රකාශ සලකන්න.
- (A) වාතය තුළ ධ්වනි වේගය වාතයේ උෂ්ණත්වය වැඩි වීමත් සමඟ වැඩි වේ.
- (B) දෙන ලද උෂ්ණත්වයක දී ලෝහයක් තුළ ධ්වනියේ වේගය වාතයේ දී එම අගයට වඩා වැඩි වේ.
- (C) ධ්වනි වේගය ධ්වනි තරංගයේ සංඛ්‍යාතය මත රඳා පවතී.
ඉහත ප්‍රකාශවලින්,
රූපයේ පෙන්වා ඇති පරිදි දුස්ස්‍රාවීතාව $\eta$ සහ ඝනකම $d$ වූ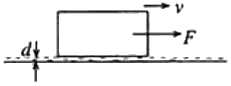
තෙල් තට්ටුවක් මත පෙට්ටියක් තබා ඇත. තෙල් සමඟ ස්පර්ශ වන, පෙට්ටියේ පෘෂ්ඨයේ වර්ගඵලය $A$ වේ. පෙට්ටිය $v$ නියත ප්‍රවේගයකින් ගමන් කරවීම සඳහා එය මත යෙදිය යුතු තිරස් බලය $F$ කුමක් විය යුතු ද?
$\ce{^235_92U}$ න්‍යෂ්ටියක් මගින් මදවේගී නියුට්‍රෝනයක් අවශෝෂණය කර පහත දක්වා ඇති විඛණ්ඩන ක්‍රියාවලිය සිදු වේ.
$\ce{ ^1_0n + ^235_92U -> ^139_56Ba + ^94_36Kr + x^1_0n }$
ඉහත විඛණ්ඩන ක්‍රියාවලියේ $x$ (සෑදෙන නියුට්‍රෝන සංඛ්‍යාව) හි අගය වන්නේ
හදවතේ මධ්‍යන්‍ය ප්‍රතිදාන පීඩනය $\pu{1.2E4 Pa}$ සහ මධ්‍යන්‍ය රුධිර ප්‍රවාහ ශිඝ්‍රතාව මිනිත්තුවට $\pu{5.0E-3 m3}$ වේ නම්, හදවතේ මධ්‍යන්‍ය ප්‍රතිදාන ක්ෂමතාව වනුයේ
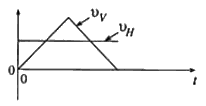
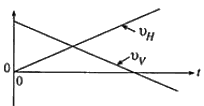
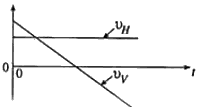
රූපයේ දැක්වෙන ආකාරයට, තිරස සමග $\theta$ කෝණයක් සාදන
දිශාවකට $v$ ප්‍රවේගයකින් වස්තුවක් ගුරුත්වාකර්ෂණය යටතේ ප්‍රක්ෂේපණය කරන ලදී. කාලය $(t)$ සමග වස්තුවේ ප්‍රවේගයේ තිරස් $(v_H)$ සහ සිරස් $(v_v)$ සංරචකයන්ගේ විචලනයන් නිවැරදිව දැක්වෙන්නේ පහත සඳහන් ප්‍රස්තාර අතුරෙන් කුමක් මගින් ද?
මලල ක්‍රීඩකයෝ දෙදෙනෙක් $v_1$ සහ $v_2$ නියත වේගයන්ගෙන් අරය $\pu{50 m}$ වූ වෘත්තාකාර ධාවන පථයක $\pu{10 km}$ තරගයක ධාවනයේ යෙදෙති. $v_1$ වේගයක් සහිත මලල ක්‍රීඩකයා රවුම් 10 ක් සම්පූර්ණ කරන විට අනෙක් මලල ක්‍රීඩකයා රවුම් 9 ක් සම්පූර්ණ කරන බව පෙනුණි. $\frac{v_1}{v_2}$ අතර අනුපාතය වන්නේ,
යන්ත්‍රයක ඇති $A$ සහ $B$ නම් රෝද දෙකක් පොදු අක්ෂයක්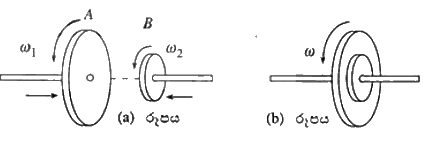
වටා පිළිවෙළින් $\omega_1$ සහ $\omega_2$ කෝණික වේගයන්ගෙන් එකම දිශාවට භ්‍රමණය වේ. $(a)$ රූපය බලන්න. භ්‍රමණ අක්ෂය වටා $A$ හි අවස්ථිති සූර්ණය $I_1$ වන අතර $B$ සඳහා එම අගය $I_2$ වේ. කිසියම් මොහොතක දී රෝද දෙක හොඳින් තද වන ලෙස එකිනෙක වෙතට ඒවා තල්ලු වන අතර පද්ධතිය ලිස්සීමකින් තොරව $\omega$ පොදු කෝණික වේගයකින් භ්‍රමණය වේ. $(b)$ රූපය බලන්න. $\omega$ හි අගය දෙනු ලබන්නේ