ඒකක පමණක් සැලකීමේ දී පහත සඳහන් කුමන රාශිය, ඉතිරි ඒවායින් වෙනස් වේ ද?
පහත කුමන රාශිය/රාශීන් මාන රහිත වේ ද?
- (A) සාපේක්ෂ ප්‍රවේශය
- (B) සාපේක්ෂ ඝනත්වය
- (C) සාපේක්ෂ ආර්ද්‍රතාවය
අන්වායාම තරංග ආකාරයට ප්‍රචාරණය වන්නේ පහත දැක්වෙන ඒවායින් කවරක් ද?
ගිටාරයක් වාදනය කරන විට එය
සංයුක්ත අන්වීක්ෂයක් සම්බන්ධ ව පහත සඳහන් ප්‍රකාශ අතුරෙන් කුමක් සත්‍ය නොවේ ද?
රූපයේ දැක්වෙන ආකාරයට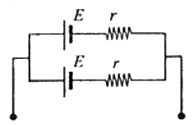
සම්බන්ධ කර ඇති, එක් එක් හි වි.ගා.බ. $E$ සහ අභ්‍යන්තර ප්‍රතිරෝධය $r$ වන කෝෂ දෙකක් සමක වන්නේ,
අරයයන් $R_1 = r$ සහ $R_2 = 2r$ වූ ආරෝපිත සන්නායක ගෝල දෙකක් සිහින් සන්නායක කම්බියක් මගින් සම්බන්ධ කරනු ලැබේ. සම්බන්ධ කළ පසු ගෝල දෙක මත ආරෝපණ පිළිවෙළින් $Q_1$ සහ $Q_2$ ද අනුරූප පෘෂ්ඨික ආරෝපණ ඝනත්ව පිළිවෙළින් $\sigma_1$ හා $\sigma_2$ ද වේ නම්, එවිට
එක් එක් හි ආරෝපණය $+q$ වූ අංශු හතරක්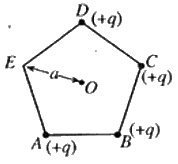
සවිධි පංචාස්‍රයක ශීර්ෂ හතරක් මත රූපයේ පෙනෙන ආකාරයට තබා ඇත. පංචාස්‍රයේ $O$ කේන්ද්‍රයේ සිට ශීර්ෂයකට ඇති දුර $a$ වේ. පංචාස්‍රයේ කේන්ද්‍රයේ විද්‍යුත් ක්ෂේත්‍ර තීව්‍රතාව
ස්කන්ධය $M$ සහ අරය $R$ වන තුනී මුදුවක් එහි කේන්ද්‍රය හරහා එහි තලයට ලම්බක ව ගමන් කරන අක්ෂයක් වටා තිරස් තලයක නියත $\omega$ කෝණික ප්‍රවේගයකින් භ්‍රමණය වෙමින් පවතී. දැන් එක් එක් හි ස්කන්ධය $m$ වූ කුඩා ස්කන්ධ දෙකක් මුදුවේ විශ්කම්භයක ප්‍රතිවිරුද්ධ කෙළවර වලට සීරුවෙන් සම්බන්ධ කළහොත් පද්ධතියේ නව කෝණික ප්‍රවේගය වන්නේ,
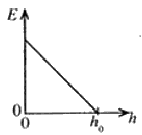
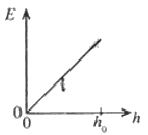
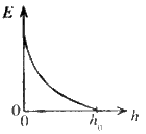
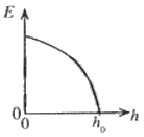
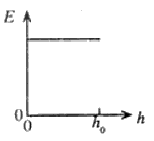
පොළොවේ සිට $h_0$ උසකින් පිහිටි ස්ථානයක සිට ස්කන්ධය $m$ වූ අංශුවක් නිදහසේ අතහරිනු ලැබේ. පොළොවේ සිට මනිනු ලබන $h$ උස සමග අංශුවේ චාලක ශක්තියේ $(E)$ විචලනය වඩාත් හොදින් නිරූපණය කරනු ලබන්නේ.
