| (a) | P හා Q මෝටර් රථ දෙකක් සෘජු පාරක් දිගේ නියත ත්වරණ සහිතව එකම දිශාවකට චලනය වේ. කාලය t=0 හි දී P හි ප්රවේගය u ms−1 ද Q හි ප්රවේගය (u+9) ms−1 ද වේ. P හි නියත ත්වරණය f ms−2 ද Q හි නියත ත්වරණය (f+110) ms−2 ද වේ. - (i) t≥0 සඳහා P හා Q හි චලිතවලට, එකම රූපයක හා
- (ii) t≥0 සඳහා P ට සාපේක්ෂව Q හි චලිතයට, වෙනම රූපයක,
ප්රවේග-කාල වක්රවල දළ සටහන් අඳින්න.
කාලය t=0 හි දී P මෝටර් රථය Q මෝටර් රථයට වඩා මීටර 200 ක් ඉදිරියෙන් සිටි බව තවදුරටත් දී ඇත. P පසුකර යෑමට Q මගින් ගනු ලබන කාලය සොයන්න. |
| (b) | සමාන්තර ඍජු ඉවුරු සහිත පළල a වූ ගගක් u ඒකාකාර ප්රවේගයෙන් ගලයි. රූපයෙහි, A,B,C හා D යන ඉවුරු මත වූ ලක්ෂ්ය සමචතුරස්රයක ශිර්ෂ වේ. ජලයට සාපේක්ෂව නියත v(>u) වේගයෙන් චලනය වන B1 හා B2 බෝට්ටු දෙකක් එකම මොහොතක A සිට ඒවායේ ගමන් ආරම්භ කරයි. B1 බෝට්ටුව පළමුව →AC දිගේ C වෙත ගොස් ඉන්පසු →CD දිශාවට ගග දිගේ ඉහළට D 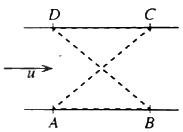 වෙත යයි. B2 බෝට්ටුව පළමුව →AB දිශාවට ගග දිගේ පහළට B වෙත ගොස් ඉන්පසු →BD දිගේ D වෙත යයි. එකම රූපයක, B1 හි A සිට C දක්වා ද B2 හි B සිට D දක්වා ද චලිත සඳහා ප්රවේග ත්රිකෝණවල දළ සටහන් අඳින්න. වෙත යයි. B2 බෝට්ටුව පළමුව →AB දිශාවට ගග දිගේ පහළට B වෙත ගොස් ඉන්පසු →BD දිගේ D වෙත යයි. එකම රූපයක, B1 හි A සිට C දක්වා ද B2 හි B සිට D දක්වා ද චලිත සඳහා ප්රවේග ත්රිකෝණවල දළ සටහන් අඳින්න.
ඒ නයින්, A සිට C දක්වා චලිතයේ දී B1 බෝට්ටුවේ වේගය 1√2(√2v2−u2+u) බව පෙන්වා B සිට D දක්වා චලිතයේ දී B2 බෝට්ටුවේ වේගය සොයන්න.
B1 හා B2 බෝට්ටු දෙකම එකම මොහොතක දී D වෙත ළගා වන බව තවදුරටත් පෙන්වන්න. |

 වෙත යයි.
වෙත යයි.