1. එක එකෙහි දිග $2a$ වන $AB, BC$ හා $CD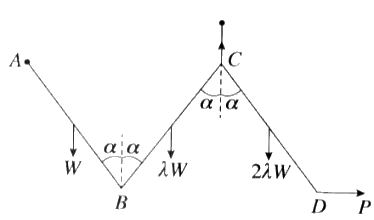$ ඒකාකාර දඬු තුනක් $B$ හා $C$ අන්තවල දී සුමට ලෙස සන්ධි කර ඇත. $AB, BC$ හා $CD$ දඬුවල බර පිළිවෙළින් $W, \lambda W$ හා $2\lambda W$ වේ. $A$ කෙළවර අචල ලක්ෂ්‍යයකට සුමට ලෙස අසව් කර ඇත. රූපයේ දැක්වෙන පරිදි දඬු සිරස් තලයක සමතුලිතව තබා ඇත්තේ $A$ හා $C$ එකම තිරස් මට්ටමේ ද දඬු එක එකක් සිරස සමග $\alpha$ කෝණයක් සාදන පරිදි ද $C$ සන්ධියට හා $C$ සන්ධියට සිරස්ව ඉහළින් වූ අචල ලක්ෂයකට ඇඳු සැහැල්ලු අවිතථ්‍ය තන්තුවක් මගින් හා $D$ අන්තයට යෙදූ තිරස් $P$ බලයක් මගිනි. $\lambda = \frac{1}{3}$ බව පෙන්වන්න.

$B$ හි දී $CB$ මගින් $AB$ මත ඇති කරන බලයේ තිරස් හා සිරස් සංරචක පිළිවෙළින් $\frac{W}{3} \tan \alpha$ හා $\frac{W}{6}$ බව ද පෙන්වන්න.

2. යාබද රූපයේ දැක්වෙන රාමු සැකිල්ල සාදා ඇත්තේ 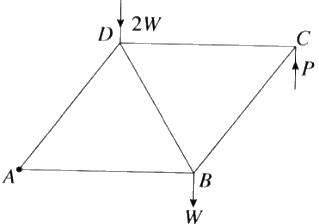$A, B, C$ හා $D$ හි දී නිදහසේ සන්ධි කරන ලද එක එකෙහි දිග $2a$ වන $AB$, $BC,CD,DA$ හා $BD$ සැහැල්ලු දඬු මගිනි. $B$ හා $D$ හි දී පිළිවෙළින් $W$ හා $2W$ වන භාර ඇත. රාමු සැකිල්ල $A$ හි දී සුමටව අචල ලක්ෂ්‍යයකට අසව් කර $AB$ තිරස්ව ඇතිව සමතුලිතතාවේ තබා ඇත්තේ $C$ හි දී සිරස්ව ඉහළට යොදන ලද $P$ බලයක් මගිනි. $W$ ඇසුරෙන් $P$ හි අගය සොයන්න.

බෝ අංකනය භාවිතයෙන්, ප්‍රත්‍යබල සටහනක් ඇඳ ඒ නයින්, දඬුවල ප්‍රත්‍යාබල ආතති ද තෙරපුම් ද යන්න සඳහන් කරමින් ඒවා සොයන්න.