තිරසට $\frac{\pi}{6}$ කෝණයකින් ආනත සුමට අචල තලයක උපරිම බෑවුම් රේඛාවක් 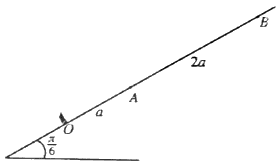මත $OA = a$ හා $AB = 2a$ වන පරිදි $O$ පහළම ලක්ෂ්‍යය ලෙස ඇතිව $O, A$ හා $B$ ලක්ෂ්‍ය එම පිළිවෙළින් පිහිටා ඇත. ස්වාභාවික දිග $a$ හා ප්‍රත්‍යස්ථතා මාපාංකය $mg$ වූ සැහැල්ලු ප්‍රත්‍යාස්ථ තන්තුවක එක් කෙළවරක් $O$ ලක්ෂයට ඇදා ඇති අතර අනෙක් කෙළවර ස්කන්ධය $m$ වූ $P$ අංශුවකට ඈඳා ඇත. $P$ අංශුව $B$ ලක්ෂ්‍යය කරා ළගා වන තෙක් තන්තුව $OAB$ රේඛාව දිගේ අදිනු ලැබේ. ඉන්පසු $P$ අංශුව නිශ්චලතාවයේ සිට මුදා හරිනු ලැබේ. $B$ සිට $A$ දක්වා $P$ හි චලිත සමීකරණය, $0 \le x \le 2a$ සදහා, $\ddot{x} + \frac{g}{a} \Big( x + \frac{a}{2} \Big) = 0$ මගින් දෙනු ලබන බව පෙන්වන්න; මෙහි $AP = x$ වේ.
$y = x + \frac{a}{2}$ යැයි ගෙන ඉහත චලිත සමීකරණය $\frac{a}{2} \le y \le \frac{5a}{2}$ සඳහා $\ddot{y} + \omega^2y = 0$ ආකාරයෙන් නැවත ලියන්න; මෙහි $\omega = \sqrt{\frac{g}{a}}$ වේ.
ඉහත සරල අනුවර්තී චලිතයේ කේන්ද්‍රය සොයා $\dot{y}^2 = \omega^2(c^2 - y^2)$ සුත්‍රය භාවිතයෙන්, $c$ විස්තාරය හා $A$ වෙත ළගා වන විට $P$ හි ප්‍රවේගය සොයන්න.
$O$ වෙත ළගා වන විට $P$ හි ප්‍රවේගය $\sqrt{7ga}$ බව පෙන්වන්න.
$B$ සිට $O$ දක්වා චලනය වීමට $P$ මගින් ගනු ලබන කාලය $\sqrt{\frac{g}{a}} \left\{ \cos^{-1} \Big( \frac{1}{5} \Big) + 2k \right\}$ බවත් පෙන්වන්න; මෙහි $k = \sqrt{7} - \sqrt{6}$ වේ.
$P$ අංශුව $O$ වෙත ළඟා වන විට, තලයට ලම්බව $O$ හි සවිකර ඇති සුමට බාධකයක් හා එය ගැටෙයි. බාධකය හා $P$ අතර ප්‍රත්‍යාගති සංගුණකය $e$ වේ. $0 < e \le \frac{1}{\sqrt{7}}$ නම්, පසුව සිදු වන $P$ හි චලිතය සරල අනුවර්තී නොවන බව පෙන්වන්න.