
- රූපයෙහි පෙන්වා ඇති පරිදි P,Q හා R දුම්රිය ස්ථාන තුනක් PQ=140 km හා QR=akm
 වන පරිදි සරල රේඛාවක පිහිටා ඇත. කාලය t=0 දී A දුම්රියක් P හි දී නිශ්චලතාවයෙන් ආරම්භ කර Q දෙසට fkmh−2 නියත ත්වරණයෙන් පැය භාගයක් ගමන් කර කාලය t=12h හි දී එයට තිබූ ප්රවේගය පැය තුනක කාලයක් පවත්වාගෙන යයි. ඉන්පසු එය fkmh−2 නියත මන්දනයෙන් ගමන් කර Q හි දී නිශ්චලතාවට පැමිණෙයි. කාලය t=1h හි දී තවත් B දුම්රියක් R හි දී නිශ්චලතාවයෙන් ආරම්භ කර Q දෙසට පැය T කාලයක් 2fkmh−2 නියත ත්වරණයෙන් ද ඉන්පසු fkmh−2 නියත මන්දනයෙන් ද ගමන් කර Q හි දී නිශ්චලතාවට පැමිණෙයි. දුම්රිය දෙක ම එක ම මෙහොතේ දී නිශ්චලතාවට පැමිණේ. එක ම රූපසටහනක A හා B හි චලිත සඳහා ප්රවේග-කාල ප්රස්තාරවල දළ සටහන් අඳින්න.
වන පරිදි සරල රේඛාවක පිහිටා ඇත. කාලය t=0 දී A දුම්රියක් P හි දී නිශ්චලතාවයෙන් ආරම්භ කර Q දෙසට fkmh−2 නියත ත්වරණයෙන් පැය භාගයක් ගමන් කර කාලය t=12h හි දී එයට තිබූ ප්රවේගය පැය තුනක කාලයක් පවත්වාගෙන යයි. ඉන්පසු එය fkmh−2 නියත මන්දනයෙන් ගමන් කර Q හි දී නිශ්චලතාවට පැමිණෙයි. කාලය t=1h හි දී තවත් B දුම්රියක් R හි දී නිශ්චලතාවයෙන් ආරම්භ කර Q දෙසට පැය T කාලයක් 2fkmh−2 නියත ත්වරණයෙන් ද ඉන්පසු fkmh−2 නියත මන්දනයෙන් ද ගමන් කර Q හි දී නිශ්චලතාවට පැමිණෙයි. දුම්රිය දෙක ම එක ම මෙහොතේ දී නිශ්චලතාවට පැමිණේ. එක ම රූපසටහනක A හා B හි චලිත සඳහා ප්රවේග-කාල ප්රස්තාරවල දළ සටහන් අඳින්න.
ඒ නයින් හෝ අන් අයුරකින් හෝ, f=80 බව පෙන්වා, T හි හා a හි අගයන් සොයන්න.
- නැවක් පොළොවට සාපේක්ෂව u ඒකාකාර වේගයෙන් බටහිර දෙසට යාත්රා කරන අතර බෝට්ටුවක් පොළොවට සාපේක්ෂව u2 ක ඒකාකාර වේගයෙන් සරල රේඛීය පෙතක යාත්රා කරයි. එක්තරා මොහොතක දී, බෝට්ටුවෙන් d දුරකින් උතුරෙන් නැගෙනහිරට π3 ක කෝණයකින් නැව පිහිටයි.
- බෝට්ටුව පොළොවට සාපේක්ෂව උතුරෙන් බටහිරට π6 ක කෝණයක් සාදන දිශාවට යාත්රා කරයි නම් බෝට්ටුවට නැව අල්ලාගත හැකි බව පෙන්වා, එයට නැව අල්ලා ගැනීමට ගතවන කාලය 2d√3u බව පෙන්වන්න.
- බෝට්ටුව පොළොවට සාපේක්ෂව උතුරෙන් නැගෙනහිරට π6 ක කෝණයක් සාදන දිශාවට යාත්රා කරයි නම් නැවට සාපේක්ෂව බෝට්ටුවේ වේගය √7u2 බව පෙන්වා, නැව සහ බෝට්ටුව අතර කෙටිම දුර d2√7 බව පෙන්වන්න.
- රූපයෙහි ABC ත්රිකෝණය, AˆCB=α,AˆBC=π2 හා AB=2a වූ BC
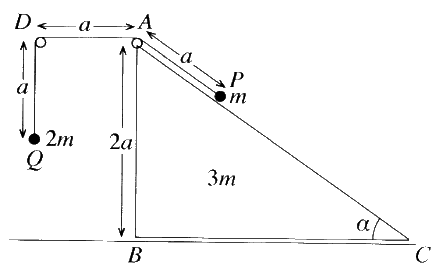 අඩංගු මුහුණත සුමට තිරස් ගෙබිමක් මත තබන ලද ස්කන්ධය 3m වන සුමට ඒකාකාර කුඤ්ඤයක ගුරුත්ව කේන්ද්රය තුළින් වූ සිරස් හරස්කඩ වේ. AC රේඛාව, එය අඩංගු මුහුණතෙහි උපරිම බෑවුම් රේඛාවක් වේ. D ලක්ෂ්යය, AD තිරස් වන පරිදි ABC තලයෙහි වූ අචල ලක්ෂ්යයකි. A හා D හි සවිකර ඇති සුමට කුඩා කප්පි දෙකක් මතින් යන දිග 3a වූ සැහැල්ලු අවිතත්ය තන්තුවක දෙකෙළවරට පිළිවෙළින් ස්කන්ධය m හා 2m වූ P හා Q අංශු දෙක ඈඳා ඇත. රූපයේ දැක්වෙන පරිදි P අංශුව AC මත අල්වා තබා AP=AD=DQ=a වන පරිදි Q අංශුව නිදහසේ එල්ලෙමින් පද්ධතිය නිශ්චලතාවයෙන් මුදා හරිනු ලැබේ. Q අංශුව ගෙබිමට ළඟා වීමට ගන්නා කාලය නිර්ණය කිරීමට ප්රමාණවත් සමීකරණ ලබා ගන්න.
අඩංගු මුහුණත සුමට තිරස් ගෙබිමක් මත තබන ලද ස්කන්ධය 3m වන සුමට ඒකාකාර කුඤ්ඤයක ගුරුත්ව කේන්ද්රය තුළින් වූ සිරස් හරස්කඩ වේ. AC රේඛාව, එය අඩංගු මුහුණතෙහි උපරිම බෑවුම් රේඛාවක් වේ. D ලක්ෂ්යය, AD තිරස් වන පරිදි ABC තලයෙහි වූ අචල ලක්ෂ්යයකි. A හා D හි සවිකර ඇති සුමට කුඩා කප්පි දෙකක් මතින් යන දිග 3a වූ සැහැල්ලු අවිතත්ය තන්තුවක දෙකෙළවරට පිළිවෙළින් ස්කන්ධය m හා 2m වූ P හා Q අංශු දෙක ඈඳා ඇත. රූපයේ දැක්වෙන පරිදි P අංශුව AC මත අල්වා තබා AP=AD=DQ=a වන පරිදි Q අංශුව නිදහසේ එල්ලෙමින් පද්ධතිය නිශ්චලතාවයෙන් මුදා හරිනු ලැබේ. Q අංශුව ගෙබිමට ළඟා වීමට ගන්නා කාලය නිර්ණය කිරීමට ප්රමාණවත් සමීකරණ ලබා ගන්න.
- රූපයේ දැක්වෙන පරිදි ABCDE සුමට තුනී කම්බියක් සිරස් තලයක සවි
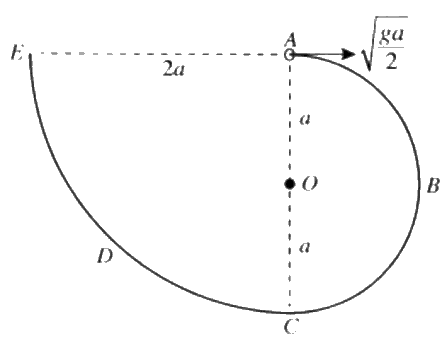 කර ඇත. ABC කොටස O කේන්ද්රය හා අරය a වූ අර්ධ වෘත්තයක් වන අතර CDE කොටස කේන්ද්රය A හා අරය 2a වූ වෘත්තයක් හතරෙන් කොටසකි. A හා C ලක්ෂ්ය O හරහා යන සිරස් රේඛාවේ පිහිටන අතර, AE රේඛාව තිරස් වේ. ස්කන්ධය m වූ කුඩා සුමට P පබළුවක් A හි තබා තිරස්ව √ga2 ප්රවේගයක් දෙනු ලබන අතර එය කම්බිය දිගේ චලිතය ආරම්භ කරයි.
කර ඇත. ABC කොටස O කේන්ද්රය හා අරය a වූ අර්ධ වෘත්තයක් වන අතර CDE කොටස කේන්ද්රය A හා අරය 2a වූ වෘත්තයක් හතරෙන් කොටසකි. A හා C ලක්ෂ්ය O හරහා යන සිරස් රේඛාවේ පිහිටන අතර, AE රේඛාව තිරස් වේ. ස්කන්ධය m වූ කුඩා සුමට P පබළුවක් A හි තබා තිරස්ව √ga2 ප්රවේගයක් දෙනු ලබන අතර එය කම්බිය දිගේ චලිතය ආරම්භ කරයි.
→OA සමග \theta (0 \le \theta \le \pi) කෝණයක් \overrightarrow{OP} සාදන විට P පබළුවේ v වේගය, v^2 = \frac{ga}{2}(5 - 4\cos \theta) මගින් දෙනු ලබන බව පෙන්වන්න.
ඉහත පිහිටීමේ දී කම්බිය මගින් P පබළුව මත ඇති කරන ප්රතික්රියාව සොයා, P පබළුව \theta = cos^{-1} (\frac{5}{6}) වූ ලක්ෂ්යය පසු කරන විට එය එහි දිශාව වෙනස් කරන බව පෙන්වන්න.
P පබළුව E හි දී කම්බියෙන් ඉවත් වීමට මොහොතකට පෙර එහි ප්රවේගය ලියා දක්වා එම මොහොතේ දී කම්බිය මගින් P පබළුව මත ඇති කරන ප්රතික්රියාව සොයන්න.
රූපයේ දැක්වෙන පරිදි AB = 2a, BC = a, CD = 2a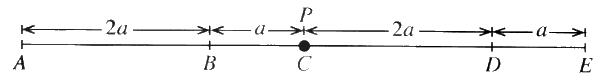 හා DE = a වන පරිදි සුමට තිරස් මේයක් මත A, B, C, D හා E ලක්ෂ්ය එම පිළිවෙළින් සරල රේඛාවක් මත පිහිටා ඇත. ස්වභාවික දිග 2a හා ප්රත්යස්ථතා මාපාංකය kmg වන සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් A ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර ස්කන්ධය m වන P අංශුවකට ඈඳා ඇත. ස්වභාවික දිග a හා ප්රත්යාස්ථතා මාපාංකය mg වන තවත් සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් E ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර P අංශුවට ඈඳා ඇත.
හා DE = a වන පරිදි සුමට තිරස් මේයක් මත A, B, C, D හා E ලක්ෂ්ය එම පිළිවෙළින් සරල රේඛාවක් මත පිහිටා ඇත. ස්වභාවික දිග 2a හා ප්රත්යස්ථතා මාපාංකය kmg වන සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් A ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර ස්කන්ධය m වන P අංශුවකට ඈඳා ඇත. ස්වභාවික දිග a හා ප්රත්යාස්ථතා මාපාංකය mg වන තවත් සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් E ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර P අංශුවට ඈඳා ඇත.
P අංශුව C හි අල්වා තබා මුදා හල විට, එය සමතුලිතතාවේ පවතී. k හි අගය සොයන්න.
දැන්, P අංශුව D ලක්ෂ්යයට ළඟා වන තෙක් AP තන්තුව ඇද නිශ්චලතාවයේ සිට මුදා හරිනු ලැබේ. D සිට B දක්වා P හි චලිත සමීකරණය \ddot{x} + \frac{3g}{a}x = 0 මගින් දෙනු ලබන බව පෙන්වන; මෙහි CP = x වේ. \dot{x}^2 = \frac{3g}{a}(c^2 – x^2) සූත්රය භාවිතයෙන් P අංශුව B ට ළඟා වන විට එහි ප්රවේගය 3\sqrt{ga} බව පෙන්වන්න; මෙහි c යනු විස්තරය වේ.
P අංශුව B වෙත ළඟා වන විට එයට ආවේගයක් දෙනු ලබන්නේ ආවේගයෙන් මොහොතකට පසු P හි ප්රවේගය \overrightarrow{BA} දිශාවට \sqrt{ag} වන පරිදි ය.
B පසු කිරීමෙන් පසු ක්ෂණික නිසලතාවට පත්වන තෙක් P හි චලිත සමීකරණය \ddot{y} + \frac{g}{a}y = 0 මගින් දෙනු ලබන බව පෙන්වන්න; මෙහි DP = y වේ. D වලින් පටන් ගත් P අංශුව දෙවන වතාවට B වෙත පැමිණීමට ගන්නා මුළු කාලය 2\sqrt{\frac{a}{g}} \left( \frac{\pi}{3\sqrt{3}} + \cos^{-1} \left( \frac{3}{\sqrt{10}} \right) \right) බව පෙන්වන්න.
- \mathbf{a} හා \mathbf{b} යනු ඒකක දෙශික දෙකක් යැයි ගනිමු.
O මූලයක් අනුබද්ධයෙන් A, B හා C ලක්ෂ්ය තුනක පිහිටුම් දෙයික පිළිවෙළින් 12\mathbf{a}, 18\mathbf{b} හා 10\mathbf{a} + 3\mathbf{b} වේ.
\mathbf{a} හා \mathbf{b} ඇසුරෙන් \overrightarrow{AC} හා \overrightarrow{CB} ප්රකාශ කරන්න. A, B හා C ඒක රේඛීය බව අපෝහනය කර, AC : CB සොයන්න. OC = \sqrt{139} බව දී ඇත. A\hat{O}B = \frac{\pi}{3} බව පෙන්වන්න.
- ABCD යනු AB = 2m හා B\hat{A}D = \frac{\pi}{3} වූ රොම්බසයකි.
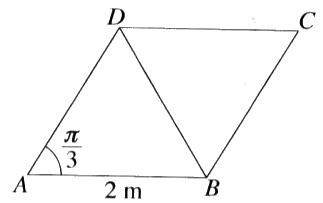 විශාලත්වය \pu{10N}, \pu{2N, 6N, PN} හා \pu{Q N} වූ බල පිළිවෙළින් AD, BA, BD, DC හා CB දිගේ අක්ෂර අනුපිළිවෙළින් දැක්වෙන දිශාවලට ක්රියා කරයි. සම්ප්රයුක්ත බලයේ විශාලත්වය \pu{10 N} ද එහි දිශාව BC ට සමාන්තර B සිට C අතට වූ දිශාව බව ද දී ඇත. P හා Q හි අගයන් සොයන්න.
විශාලත්වය \pu{10N}, \pu{2N, 6N, PN} හා \pu{Q N} වූ බල පිළිවෙළින් AD, BA, BD, DC හා CB දිගේ අක්ෂර අනුපිළිවෙළින් දැක්වෙන දිශාවලට ක්රියා කරයි. සම්ප්රයුක්ත බලයේ විශාලත්වය \pu{10 N} ද එහි දිශාව BC ට සමාන්තර B සිට C අතට වූ දිශාව බව ද දී ඇත. P හා Q හි අගයන් සොයන්න.
සම්ප්රයුක්ත බලයෙහි ක්රියා රේඛාව, දික් කරන ලද BA හමුවන ලක්ෂයට A සිට ඇති දුර ද සොයන්න.
දැන්, සම්ප්රයුක්ත බලය A හා C ලක්ෂ්ය හරහා යන පරිදි වාමාවර්ත අතට ක්රියා කරන සූර්ණය \pu{M Nm} වූ යුමයක් ද CB හා DC දිගේ අක්ෂර අනුපිළිවෙළින් දැක්වෙන දිශාවලට ක්රියා කරන එක එකෙහි විශාලත්වය \pu{F N} වූ බල දෙකක් ද පද්ධතියට එකතු කරනු ලැබේ. F හා M හි අගයන් සොයන්න.
- එක එකෙහි දිග 2a වන AB, BC හා CD
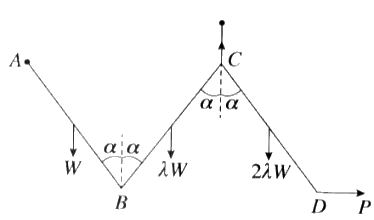 ඒකාකාර දඬු තුනක් B හා C අන්තවල දී සුමට ලෙස සන්ධි කර ඇත. AB, BC හා CD දඬුවල බර පිළිවෙළින් W, \lambda W හා 2\lambda W වේ. A කෙළවර අචල ලක්ෂ්යයකට සුමට ලෙස අසව් කර ඇත. රූපයේ දැක්වෙන පරිදි දඬු සිරස් තලයක සමතුලිතව තබා ඇත්තේ A හා C එකම තිරස් මට්ටමේ ද දඬු එක එකක් සිරස සමග \alpha කෝණයක් සාදන පරිදි ද C සන්ධියට හා C සන්ධියට සිරස්ව ඉහළින් වූ අචල ලක්ෂයකට ඇඳු සැහැල්ලු අවිතථ්ය තන්තුවක් මගින් හා D අන්තයට යෙදූ තිරස් P බලයක් මගිනි. \lambda = \frac{1}{3} බව පෙන්වන්න.
ඒකාකාර දඬු තුනක් B හා C අන්තවල දී සුමට ලෙස සන්ධි කර ඇත. AB, BC හා CD දඬුවල බර පිළිවෙළින් W, \lambda W හා 2\lambda W වේ. A කෙළවර අචල ලක්ෂ්යයකට සුමට ලෙස අසව් කර ඇත. රූපයේ දැක්වෙන පරිදි දඬු සිරස් තලයක සමතුලිතව තබා ඇත්තේ A හා C එකම තිරස් මට්ටමේ ද දඬු එක එකක් සිරස සමග \alpha කෝණයක් සාදන පරිදි ද C සන්ධියට හා C සන්ධියට සිරස්ව ඉහළින් වූ අචල ලක්ෂයකට ඇඳු සැහැල්ලු අවිතථ්ය තන්තුවක් මගින් හා D අන්තයට යෙදූ තිරස් P බලයක් මගිනි. \lambda = \frac{1}{3} බව පෙන්වන්න.
B හි දී CB මගින් AB මත ඇති කරන බලයේ තිරස් හා සිරස් සංරචක පිළිවෙළින් \frac{W}{3} \tan \alpha හා \frac{W}{6} බව ද පෙන්වන්න.
- යාබද රූපයේ දැක්වෙන රාමු සැකිල්ල සාදා ඇත්තේ
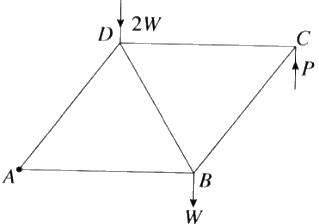 A, B, C හා D හි දී නිදහසේ සන්ධි කරන ලද එක එකෙහි දිග 2a වන AB, BC,CD,DA හා BD සැහැල්ලු දඬු මගිනි. B හා D හි දී පිළිවෙළින් W හා 2W වන භාර ඇත. රාමු සැකිල්ල A හි දී සුමටව අචල ලක්ෂ්යයකට අසව් කර AB තිරස්ව ඇතිව සමතුලිතතාවේ තබා ඇත්තේ C හි දී සිරස්ව ඉහළට යොදන ලද P බලයක් මගිනි. W ඇසුරෙන් P හි අගය සොයන්න.
A, B, C හා D හි දී නිදහසේ සන්ධි කරන ලද එක එකෙහි දිග 2a වන AB, BC,CD,DA හා BD සැහැල්ලු දඬු මගිනි. B හා D හි දී පිළිවෙළින් W හා 2W වන භාර ඇත. රාමු සැකිල්ල A හි දී සුමටව අචල ලක්ෂ්යයකට අසව් කර AB තිරස්ව ඇතිව සමතුලිතතාවේ තබා ඇත්තේ C හි දී සිරස්ව ඉහළට යොදන ලද P බලයක් මගිනි. W ඇසුරෙන් P හි අගය සොයන්න.
බෝ අංකනය භාවිතයෙන්, ප්රත්යබල සටහනක් ඇඳ ඒ නයින්, දඬුවල ප්රත්යාබල ආතති ද තෙරපුම් ද යන්න සඳහන් කරමින් ඒවා සොයන්න.
- පතුලේ අරය r ද හා උස h වූ ඒකාකාර ඝන ඍජු වෘත්තාකාර කේතුවක ස්කන්ධ කේන්ද්රය පතුලේ කේන්ද්රයේ සිට \frac{h}{4} දුරකින් ද
- අරය r ද වන ඒකාකාර ඝන අර්ධගෝලයක ස්කන්ධ කේන්ද්රය, කේන්ද්රයේ සිට \frac{3r}{8} දුරකින් ද පිහිටන බව පෙන්වන්න.
පතුලේ අරය 2a හා උස 4a ඒකාකාර ඝන ඍජු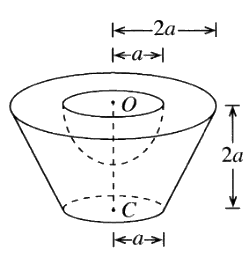 වෘත්ත කේතුවක ජින්නකයකින් ඝන අර්ධ ගෝලයක් ඉවත් කර සාදා ඇති S වංගෙඩියක් යාබද රූපයේ දැක්වේ. ජින්නකයේ ඉහළ වෘත්තාකාර මුහුණත අරය හා කේන්ද්රය පිළිවෙළින් 2a හා O වන අතර පහළ වෘත්තාකාර මුහුණත සඳහා ඒවා පිළිවෙළින් a හා C වේ. ජින්නකයේ උස 2a වේ. ඉවත් කළ ඝන අර්ධ ගෝලයෙහි අරය හා කේන්ද්රය පිළිවෙළින් a හා O වේ.
වෘත්ත කේතුවක ජින්නකයකින් ඝන අර්ධ ගෝලයක් ඉවත් කර සාදා ඇති S වංගෙඩියක් යාබද රූපයේ දැක්වේ. ජින්නකයේ ඉහළ වෘත්තාකාර මුහුණත අරය හා කේන්ද්රය පිළිවෙළින් 2a හා O වන අතර පහළ වෘත්තාකාර මුහුණත සඳහා ඒවා පිළිවෙළින් a හා C වේ. ජින්නකයේ උස 2a වේ. ඉවත් කළ ඝන අර්ධ ගෝලයෙහි අරය හා කේන්ද්රය පිළිවෙළින් a හා O වේ.
S වංගෙඩියේ ස්කන්ධ කේන්ද්රය O සිට \frac{41}{48}a දුරකින් පිහිටන බව පෙන්වන්න.
S වංගෙඩිය, එහි පහළ වෘත්තාකාර මුහුණත, 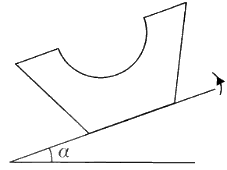 තලය ස්පර්ශ කරමින් රළු තිරස් තලයක් මත තබා ඇත. දැන්, තලය සෙමෙන් උඩු අතට ඇල කරනු ලැබේ. වංගෙඩිය හා තලය අතර ඝර්ෂණ සංගුණකය 0.9 වේ. \alpha < \tan^{-1}(0.9) නම්, වංගෙඩිය සමතුලිතතාවේ පවතින බව පෙන්වන්න; මෙහි \alpha යනු තලයේ තිරසට ආනතිය වේ.
තලය ස්පර්ශ කරමින් රළු තිරස් තලයක් මත තබා ඇත. දැන්, තලය සෙමෙන් උඩු අතට ඇල කරනු ලැබේ. වංගෙඩිය හා තලය අතර ඝර්ෂණ සංගුණකය 0.9 වේ. \alpha < \tan^{-1}(0.9) නම්, වංගෙඩිය සමතුලිතතාවේ පවතින බව පෙන්වන්න; මෙහි \alpha යනු තලයේ තිරසට ආනතිය වේ.
- එක්තරා කර්මාන්තශාලාවක අයිතමවලින් 50\% ක් A යන්ත්රය නිපදවන අතර ඉතිරිය B හා C යන්ත්ර මගින් නිපදවනු ලැබේ. A, B හා C යන්ත්ර මගින් නිපදවනු ලබන අයිතමවලින් පිළිවෙළින් 1\%, 3\% හා 2\% ක් දෝෂ සහිත බව දනිමු. සසම්භාවීව තෝරාගත් අයිතමයක් දෝෂ සහිත වීමේ සම්භාවිතාව 0.018 බව දී ඇත. B හා C යන්ත්ර මගින් නිපදවනු ලබන අයිතමවල ප්රතිශත සොයන්න.
සසම්භාවී ලෙස තෝරාගත් අයිතමයක් දෝෂ සහිත බව දී ඇති විට, එය A යන්ත්රය මගින් නිපදවන ලද එකක් වීමේ සම්භාවිතාව සොයන්න.
- එක්තරා කර්මාන්තශාලාවක සේවකයින් 100 දෙනකු තම නිවසේ සිට සේවා ස්ථානයට ගමන් කිරීමට ගනු ලබන කාලය (මිනිත්තුවලින්) පහත වගුවේ දී ඇත:
| සේවකයින් ගණන් | ගනු ලබන කාලය |
| 0-20 | 10 |
| 20-40 | 30 |
| 40-60 | 40 |
| 60-80 | 10 |
| 80-100 | 10 |
ඉහත දී ඇති ව්යාප්තියේ මධ්යන්යය, සම්මත අපගමනය හා මාතය නිමානය කරන්න.
පසුව, 80 - 100 පන්ති ප්රාන්තරයේ සිටි සියලු ම සේවකයින් කර්මාන්තශාලාව ආසන්නයේ පදිංචියට ගොස් ඇත. එයින්, 80 - 100 පන්ති ප්රාන්තරයේ සංඛ්යාතය 10 සිට 0 දක්වා ද 0-20 පන්ති ප්රාන්තරයේ සංඛ්යාතය 10 සිට 20 දක්වා ද වෙනස් විය.
නව ව්යාප්තියේ මධ්යන්යය, සම්මත අපගමනය හා මාතය නිමානය කරන්න.
