(12)
- රූපයෙහි $ABC$ ත්‍රිකෝණය, $A\hat{C}B = \alpha, A\hat{B}C = \frac{\pi}{2}$ හා $AB = 2a$ වූ $BC$
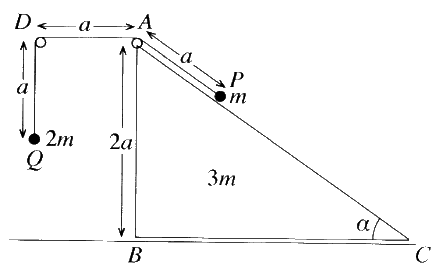අඩංගු මුහුණත සුමට තිරස් ගෙබිමක් මත තබන ලද ස්කන්ධය $3m$ වන සුමට ඒකාකාර කුඤ්ඤයක ගුරුත්ව කේන්ද්‍රය තුළින් වූ සිරස් හරස්කඩ වේ. $AC$ රේඛාව, එය අඩංගු මුහුණතෙහි උපරිම බෑවුම් රේඛාවක් වේ. $D$ ලක්ෂ්‍යය, $AD$ තිරස් වන පරිදි $ABC$ තලයෙහි වූ අචල ලක්ෂ්‍යයකි. $A$ හා $D$ හි සවිකර ඇති සුමට කුඩා කප්පි දෙකක් මතින් යන දිග $3a$ වූ සැහැල්ලු අවිතත්‍ය තන්තුවක දෙකෙළවරට පිළිවෙළින් ස්කන්ධය $m$ හා $2m$ වූ $P$ හා $Q$ අංශු දෙක ඈඳා ඇත. රූපයේ දැක්වෙන පරිදි $P$ අංශුව $AC$ මත අල්වා තබා $AP = AD = DQ = a$ වන පරිදි $Q$ අංශුව නිදහසේ එල්ලෙමින් පද්ධතිය නිශ්චලතාවයෙන් මුදා හරිනු ලැබේ. $Q$ අංශුව ගෙබිමට ළඟා වීමට ගන්නා කාලය නිර්ණය කිරීමට ප්‍රමාණවත් සමීකරණ ලබා ගන්න.
- රූපයේ දැක්වෙන පරිදි $ABCDE$ සුමට තුනී කම්බියක් සිරස් තලයක සවි
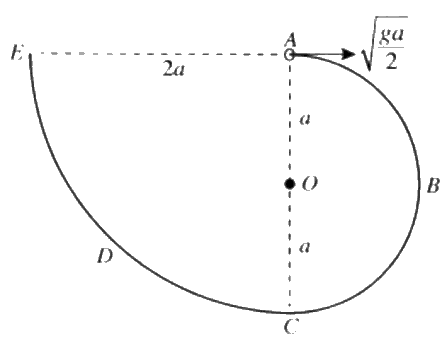කර ඇත. $ABC$ කොටස $O$ කේන්ද්‍රය හා අරය $a$ වූ අර්ධ වෘත්තයක් වන අතර $CDE$ කොටස කේන්ද්‍රය $A$ හා අරය $2a$ වූ වෘත්තයක් හතරෙන් කොටසකි. $A$ හා $C$ ලක්ෂ්‍ය $O$ හරහා යන සිරස් රේඛාවේ පිහිටන අතර, $AE$ රේඛාව තිරස් වේ. ස්කන්ධය $m$ වූ කුඩා සුමට $P$ පබළුවක් $A$ හි තබා තිරස්ව $\sqrt{\frac{ga}{2}}$ ප්‍රවේගයක් දෙනු ලබන අතර එය කම්බිය දිගේ චලිතය ආරම්භ කරයි.
$\overrightarrow{OA}$ සමග $\theta (0 \le \theta \le \pi)$ කෝණයක් $\overrightarrow{OP}$ සාදන විට $P$ පබළුවේ $v$ වේගය, $v^2 = \frac{ga}{2}(5 - 4\cos \theta)$ මගින් දෙනු ලබන බව පෙන්වන්න.
ඉහත පිහිටීමේ දී කම්බිය මගින් $P$ පබළුව මත ඇති කරන ප්‍රතික්‍රියාව සොයා, $P$ පබළුව $\theta = cos^{-1} (\frac{5}{6})$ වූ ලක්ෂ්‍යය පසු කරන විට එය එහි දිශාව වෙනස් කරන බව පෙන්වන්න.
$P$ පබළුව $E$ හි දී කම්බියෙන් ඉවත් වීමට මොහොතකට පෙර එහි ප්‍රවේගය ලියා දක්වා එම මොහොතේ දී කම්බිය මගින් $P$ පබළුව මත ඇති කරන ප්‍රතික්‍රියාව සොයන්න.
Complexity: (0)