රූපයේ දැක්වෙන පරිදි AB=2a,BC=a, CD=2a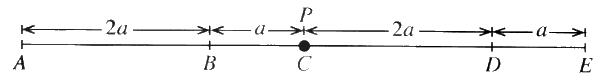 හා DE=a වන පරිදි සුමට තිරස් මේයක් මත A,B,C,D හා E ලක්ෂ්ය එම පිළිවෙළින් සරල රේඛාවක් මත පිහිටා ඇත. ස්වභාවික දිග 2a හා ප්රත්යස්ථතා මාපාංකය kmg වන සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් A ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර ස්කන්ධය m වන P අංශුවකට ඈඳා ඇත. ස්වභාවික දිග a හා ප්රත්යාස්ථතා මාපාංකය mg වන තවත් සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් E ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර P අංශුවට ඈඳා ඇත.
හා DE=a වන පරිදි සුමට තිරස් මේයක් මත A,B,C,D හා E ලක්ෂ්ය එම පිළිවෙළින් සරල රේඛාවක් මත පිහිටා ඇත. ස්වභාවික දිග 2a හා ප්රත්යස්ථතා මාපාංකය kmg වන සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් A ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර ස්කන්ධය m වන P අංශුවකට ඈඳා ඇත. ස්වභාවික දිග a හා ප්රත්යාස්ථතා මාපාංකය mg වන තවත් සැහැල්ලු ප්රත්යස්ථ තන්තුවක එක් කෙළවරක් E ලක්ෂ්යයට ඇඳා ඇති අතර අනෙක් කෙළවර P අංශුවට ඈඳා ඇත.
P අංශුව C හි අල්වා තබා මුදා හල විට, එය සමතුලිතතාවේ පවතී. k හි අගය සොයන්න.
දැන්, P අංශුව D ලක්ෂ්යයට ළඟා වන තෙක් AP තන්තුව ඇද නිශ්චලතාවයේ සිට මුදා හරිනු ලැබේ. D සිට B දක්වා P හි චලිත සමීකරණය ¨x+3gax=0 මගින් දෙනු ලබන බව පෙන්වන; මෙහි CP=x වේ. ˙x2=3ga(c2–x2) සූත්රය භාවිතයෙන් P අංශුව B ට ළඟා වන විට එහි ප්රවේගය 3√ga බව පෙන්වන්න; මෙහි c යනු විස්තරය වේ.
P අංශුව B වෙත ළඟා වන විට එයට ආවේගයක් දෙනු ලබන්නේ ආවේගයෙන් මොහොතකට පසු P හි ප්රවේගය →BA දිශාවට √ag වන පරිදි ය.
B පසු කිරීමෙන් පසු ක්ෂණික නිසලතාවට පත්වන තෙක් P හි චලිත සමීකරණය ¨y+gay=0 මගින් දෙනු ලබන බව පෙන්වන්න; මෙහි DP=y වේ. D වලින් පටන් ගත් P අංශුව දෙවන වතාවට B වෙත පැමිණීමට ගන්නා මුළු කාලය 2√ag(π3√3+cos−1(3√10)) බව පෙන්වන්න.
(13)
Complexity: (0)
