(17)
- sinA,cosA,sinB හා cosB ඇසුරෙන් sin(A−B) ලියා දක්වන්න.
- \sin (90° - \theta) = \cos \theta, හා
- 2\sin 10° = \cos 20° - \sqrt{3} \sin 20°
බව අපෝහනය කරන්න.
- සුපුරුදු අංකනයෙන්, ABC ත්රිකෝණයක් සඳහා සයින් නීතිය ප්රකාශ කරන්න.
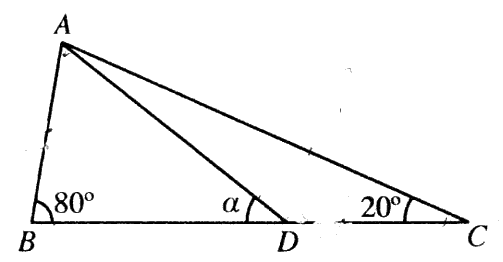
රූපයේ දක්වා ඇති ABC ත්රිකෝණයේ A\hat{B}C = 80° හා A\hat{C}B = 20° වේ. D ලක්ෂය BC මත පිහිටා ඇත්තේ AB = DC වන පරිදි ය. A\hat{D}B = \alpha යැයි ගනිමු.
සුදුසු ත්රිකෝණ සඳහා සයින් නීතිය භාවිතයෙන්, \sin 80° \sin (\alpha-20°) = \sin 20° \sin \alpha බව පෙන්වන්න.
\sin 80° = \cos 10° වන්නේ ඇයිදැයි පැහැදිලි කර, ඒ නයින්, \tan\alpha = \frac{\sin 20°}{\cos 20° - 2\sin 10°}බව පෙන්වන්න.
ඉහත (a)(ii) හි ප්රතිඵලය භාවිතයෙන් \alpha = 30° බව අපෝහනය කරන්න.
- \tan^{-1} (cos^2x) + tan^{-1}(sin x) = \frac{\pi}{4} සමීකරණය විසඳන්න.
Complexity: (0)
