1. $f(x) = x^2 + px + c$ හා $g(x) = 2x^2 + qx + c$ යැයි ගනිමු; මෙහි $p,q \in \mathbb{R}$ හා $c>0$ වේ. $f(x) = 0$ හා $g(x) = 0$ සඳහා $\alpha$ පොදු මූලයක් ඇති බව දී ඇත. $\alpha = p - q$ බව පෙන්වන්න. $p$ හා $q$ ඇසුරෙන් $c$ සොයා,

• (i) $p > 0$ නම් $p < q <2p$ බව,
• (ii) $f(x) = 0$ හි විවේචකය $(3p - 2q)^2$ බව

අපෝහනය කරන්න. $\beta$ හා $\gamma$ යනු පිළිවෙළින් $f(x) = 0$ හි හා $g(x) = 0$ හි අනික් මූල යැයි ගනිමු. $\beta = 2\gamma$ බව පෙන්වන්න. තව ද $\beta$ හා $\gamma$ මූල වන වර්ගජ සමීකරණය $2x^2 + 3(2p-p)x + (2p-q)^2 = 0$ මගින් දෙනු ලබන බව පෙන්වන්න.

2. $h(x) = x^3 + ax^2 + bx+c$ යැයි ගනිමු; මෙහි $a, b, c \in \mathbb{R}$ වේ. $x^2 - 1$ යන්න $h(x)$ හි සාධකයක් බව දී ඇත. $b = -1$ බව පෙන්වන්න. $h(x)$ යන්න $x^2 - 2x$ මගින් බෙදූ විට ශේෂය $5x + k$ බව ද දී ඇත; මෙහි $k\in \mathbb{R}$ වේ. $k$ හි අගය සොයා $h(x)$ යන්න $(x-\lambda)^2 (x - \mu)$ ආකාරයෙන් ලිවිය හැකි බව පෙන්වන්න; මෙහි $\lambda, \mu \in \mathbb{R}$ වේ.

1. පියානෝ වාදකයින් පස්දෙනකු, ගිටාර් වාදකයින් පස්දෙනකු, ගායිකාවන් තුන්දෙනකු හා ගායකයින් හත්දෙනකු අතුරෙන් හරියටම පියානෝ වාදකයින් දෙදෙනකු ද අඩු තරමින් ගිටාර් වාදකයින් හතරදෙනකු ද ඇතුළත් වන පරිදි සාමාජිකයන් එකොළොස්දෙනකුගෙන් සමන්විත සංගීත කණ්ඩායමක් තෝරා ගැනීමට අවශ්‍යව ඇත. තෝරා ගත හැකි එවැනි වෙනස් සංගීත කණ්ඩායම් ගණන සොයන්න.

මේවා අතුරෙන් හරියටම ගායිකාවන් දෙදෙනකු සිටින සංගීත කණ්ඩායම් ගණන ද සොයන්න.

2. $r \in \mathbb{Z^+}$ සඳහා $U_r = \frac{3r - 2}{r(r+1)(r+2)}$ හා $V_r = \frac{A}{r+1} - \frac{B}{r}$ යැයි ගනිමු; මෙහි $A, B \in \mathbb{R}$ වේ. $r \in \mathbb{Z^+}$ සඳහා $U_r = V_r - V_{r+1}$ වන පරිදි $A$ හා $B$ හි අගයන් සොයන්න.

ඒ නයින්, $n \in \mathbb{Z^+}$ සඳහා $\sum\limits_{r=1}^{n}{\frac{n^2}{(n+1)(n+2)}}$ බව පෙන්වන්න.
$\sum\limits_{r=1}^{\infty}{U_r}$ අපරිමිත ශ්‍රේණිය අභිසාරී බව පෙන්වා එහි ඓක්‍යය සොයන්න.
දැන්, $r \in \mathbb{Z^+}$ සඳහා $W_r = U_{r+1} - 2U_r$ යැයි ගනිමු. $\sum\limits_{r=1}^{n}{W_r} = U_{n+1} - U_1 -\sum\limits_{r=1}^{n}{U_r}$ බව පෙන්වන්න.
$\sum\limits_{r=1}^{\infty}{W_r}$ අපරිමිත ශ්‍රේණිය අභිසාරී බව අපෝහනය කර එහි ඓක්‍යය සොයන්න.

1. $A = \begin{pmatrix} a + 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{pmatrix}$, $B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ a & 2 \end{pmatrix}$ හා $C = \begin{pmatrix} a & 1 \\ a & 2\end{pmatrix}$ යැයි ගනිමු; මෙහි $a \in \mathbb{R}$ වේ. $A^TB - I = C$ බව පෙන්වන්න; මෙහි $I$ යනු ගණය 2 වන ඒකක න්‍යාසය වේ. $C^{-1}$ පවතින්නේ $a \neq 0$ ම නම් පමණක් බව ද පෙන්වන්න.

දැන්, $a = 1$ යැයි ගනිමු. $C^{-1}$ ලියා දක්වන්න.
$CPC = 2I + C$ වන පරිදි $P$ න්‍යාසය සොයන්න.

2. $z,w \in \mathbb{C}$ යැයි ගනිමු. $|z|^2 = z\bar{z}$ බව පෙන්වා, එය $z - w$ ට යෙදීමෙන්

$|z – w|^2 = |z|^2 - 2Rez\bar{w} + |w|^2$ බව පෙන්වන්න.

$|1 - z\bar{w}|^2$ සඳහා ද එවැනි ප්‍රකාශනයක්ලියා දක්වා, $|z - w|^2 - |1 - z\bar{w}|^2 = - (1- |z|^2)(1-|w|^2)$ බව පෙන්වන්න.

$|w| = 1$ හා $z \neq w$ නම් $\left| \frac{z-w}{1-z\bar{w}} \right| = 1$ බව අපෝහනය කරන්න.

3. $1 + \sqrt{3}i$ යන්න $r( \cos \theta + i \sin \theta)$ ආකාරයෙන් ප්‍රකාශ කරන්න; මෙහි $r > 0$ හා $0 < \theta < \frac{\pi}{2}$ වේ. 

$(1 + \sqrt{3}i)^m(1-\sqrt{3}i)^n = 2^8$ බව දී ඇත; මෙහි $m$ හා $n$ ධන නිඛිල වේ. ද මුවාවර් ප්‍රමේයය යෙදීමෙන්, $m$ හා $n$ හි අගයන් නිර්ණය කිරීමට ප්‍රමාණවත් සමීකරණ ලබා ගන්න.

1. $x \neq 3$ සඳහා $f(x) = \frac{x(2x - 3)}{(x-3)^2}$ යැයි ගනිමු.

$f(x)$ හි ව්‍යුත්පන්නය, $f'(x)$ යන්න $x \neq 3$ සඳහා $f'(x) = \frac{9(1-x)}{(x-3)^3}$ මගින් දෙනු ලබන බව පෙන්වන්න. ඒ නයින්, $f(x)$ වැඩි වන ප්‍රාන්තරය හා $f(x)$ අඩු වන ප්‍රාන්තර සොයන්න.
$f(x)$ හි හැරුම් ලක්ෂයේ ඛණ්ඩාංක ද සොයන්න.
ස්පර්ශෝන්මුඛ, හැරුම් ලක්ෂ්‍යය හා $x-$අන්තඃඛණ්ඩ දක්වමින් $y = f(x)$ හි ප්‍රස්තාරයේ දළ සටහනක් අඳින්න.
ප්‍රස්තාරය භාවිතයෙන්, $\frac{1}{1 + f(r)} \leq \frac{1}{3}$ අසමානතාව තෘප්ත කරන $x$ හි සියලු ම තාත්ත්වික අගයන් සොයන්න.

2. යාබද රූපයෙන් දූවිලි එකතු කරනයක මිට රහිත කොටස දැක්වේ. සෙන්ටිමීටරවලින් එහි මාන රූපයේ දැක්වේ. එහි පරිමාව $\pu{x^2h cm3}$ යන්න $\pu{450 cm3}$ බව දී ඇත. එහි පෘෂ්ඨ වර්ගඵලය $\pu{S cm2}$ යන්න $S = 2x^2 + 3xh$ මගින් දෙනු ලැබේ. $S$ අවම වන්නේ $x = 15$ වන විට බව පෙන්වන්න.

1. සියලු $x \in \mathbb{R}$ සඳහා $x^3 + 13x - 16 = A (x^2 +9)(x+1) + B(x^2 + 9) + 2(x+1)^2$ වන පරිදි $A$ හා $B$ නියත පවතින බව දී ඇත.

$A$ හා $B$ හි අගයන් සොයන්න. ඒ නයින්, $\frac{x^3 + 13x - 16}{(x+1)^2(x^2+9)}$ යන්න භින්න භාගවලින් ලියා දක්වා,
$\int{\frac{x^3 + 13x - 16}{(x+1)^2(x^2+9)} dx}$ සොයන්න.

2. කොටස් වශයෙන් අනුකලනය භාවිතයෙන්, $\int\limits_{0}^{1}{e^x\sin^2\pi x dx}$ අගයන්න.
3. $a$ නියතයක් වන $\int\limits_{0}^{a}{f(x) dx} = \int\limits_{0}^{a}{f(a - x) dx}$ සූත්‍රය භාවිතයෙන්, $\int\limits_0^{\pi}{x \cos^6x \sin^3x} dx = \frac{\pi}{2} \int\limits_0^{\pi}{x \cos^6x \sin^3x} dx$ බව පෙන්වන්න. ඒ නයින්, $\int\limits_0^{\pi}{x \cos^6x \sin^3x} dx = \frac{2\pi}{63}$ බව පෙන්වන්න.

$A \equiv (1,2)$ හා $B \equiv (3, 3)$ යැයි ගනිමු.
$A$ හා $B$ ලක්ෂ හරහා යන සරල රේඛාවේ සමීකරණය සොයන්න.
එක එකක් $l$ සමග $\frac{\pi}{4}$ ක සුළු කෝණයක් සාදමින් $A$ හරහා යන $l_1$ හා $l_2$ සරල රේඛාවල සමීකරණ සොයන්න.
$l$ මත ඕනෑම ලක්ෂයක බණ්ඩාක $(1 + 2t, 2+t)$ ආකාරයෙන් ලිවිය හැකි බව පෙන්වන්න; මෙහි $t \in \mathbb{R}$ වේ. පෙන්වන්න.
$l_1$ හා $l_2$ යන දෙකම ස්පර්ශ කරන හා කේන්ද්‍රය $l$ මත වූ මුළුමනින්ම පළමුවන වෘත්ත පාදකයේ පිහිටන අරය $\frac{\sqrt{10}}{2}$ වන. $C_1$ වෘත්තයේ සමීකරණය $x^2 + y^2 – 6x - 6y + \frac{13}{2} =0$ බව ද පෙන්වන්න.
විෂ්කම්භයක අන්ත $A$ හා $B$ වූ $C_2$ වෘත්තයේ සමීකරණය ලියා දක්වන්න.
$C_1$ හා $C_2$ වෘත්ත ප්‍රලම්බව ඡේදනය වේ දැයි නිර්ණය කරන්න.

1. $\sin A, \cos A, \sin B$ හා $\cos B$ ඇසුරෙන් $\sin (A - B)$ ලියා දක්වන්න.
   1. $\sin (90° - \theta) = \cos \theta$, හා
   2. $2\sin 10° = \cos 20° - \sqrt{3} \sin 20°$

බව අපෝහනය කරන්න.

2. සුපුරුදු අංකනයෙන්, $ABC$ ත්‍රිකෝණයක් සඳහා සයින් නීතිය ප්‍රකාශ කරන්න.

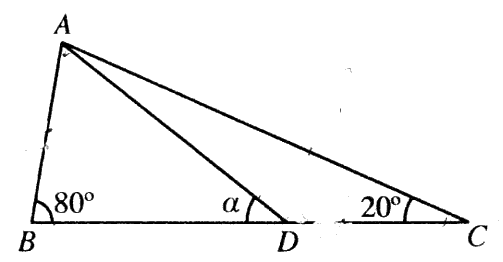
රූපයේ දක්වා ඇති $ABC$ ත්‍රිකෝණයේ $A\hat{B}C = 80°$ හා $A\hat{C}B = 20°$ වේ. $D$ ලක්ෂය $BC$ මත පිහිටා ඇත්තේ $AB = DC$ වන පරිදි ය. $A\hat{D}B = \alpha$ යැයි ගනිමු.

සුදුසු ත්‍රිකෝණ සඳහා සයින් නීතිය භාවිතයෙන්, $\sin 80° \sin (\alpha-20°) = \sin 20° \sin \alpha$ බව පෙන්වන්න.
$\sin 80° = \cos 10°$ වන්නේ ඇයිදැයි පැහැදිලි කර, ඒ නයින්, $\tan\alpha = \frac{\sin 20°}{\cos 20° - 2\sin 10°}$බව පෙන්වන්න.
ඉහත $(a)(ii)$ හි ප්‍රතිඵලය භාවිතයෙන් $\alpha = 30°$ බව අපෝහනය කරන්න.

3. $\tan^{-1} (cos^2x) + tan^{-1}(sin x) = \frac{\pi}{4}$ සමීකරණය විසඳන්න.