ඉලෙක්ට්‍රෝන වෝල්ට $(\mathrm{eV})$ යනු
පහත සඳහන් $A$, $B$ සහ $C$ යන මිනුම්, නිවැරදි ලෙස තෝරා ගත් මිනුම් උපකරණ භාවිතයෙන් ලබා ගෙන ඇත.
$A=3.1\ \mathrm{cm}$ $B = 4.23\ \mathrm{cm}$ $C = 0.354\ \mathrm{cm}$
$A$, $B$ සහ $C$ යන මිනුම් සඳහා යොදා ගෙන ඇති උපකරණ වනුයේ
| A | B | C | |
| (1) | ව'නියර් කැලිපරය | ව'නියර් කැලිපරය | මයික්‍රෝමීටර ඉස්කුරුප්පු ආමානය |
| (2) | මීටර කෝදුව | මීටර කෝදුව | ව'නියර් කැලිපරය |
| (3) | මීටර කෝදුව | මයික්‍රෝමීටර ඉස්කුරුප්පු ආමානය | චල අණ්වීක්ෂය |
| (4) | මීටර කෝදුව | ව'නියර් කැලිපරය | මයික්‍රෝමීටර ඉස්කුරුප්පු ආමානය |
| (5) | ව'නියර් කැලිපරය | මීටර කෝදුව | චල අණ්වීක්ෂය |
ව'නියර් කැලිපරය මයික්‍රෝමීටර ඉස්කුරුප්පු ආමානය මීටර කෝදුව චල අණ්වීක්ෂය
එක එකෙහි බල්බය තුළ සමාන රසදිය පරිමාවන් ඇති $A$ සහ $B$ රසදිය විදුරු උෂ්ණත්වමාන දෙකක කේශික නලවල අරයයත් පිළිවෙළින් $r$ සහ $\frac{r}{3}$ වේ. බල්බවල උෂ්ණත්ව $1\ \mathrm{°C}$ කින් වැඩි කළ විට
යන අනුපාතය ආසන්න වශයෙන් (වීදුරුවල ප්‍රසාරණය නොසලකා හරින්න.)
ධ්වනි තීව්‍රතා මට්ටම $1\ \mathrm{dB}$ කින් ඉහළ නැංවූයේ නම්, ධ්වනි තීව්‍රතාව කොපමණ සාධකයකින් වැඩි වේ ද?
ප්‍රකාශ උපකරණ තුනක් පිළිබඳ ව කර ඇති පහත සඳහන් ප්‍රකාශ සලකා බලන්න.
- (A) සරල අණ්වීක්ෂයට එක් අභිසාරී කාචයක් ඇති අතර, අණ්වීක්ෂය සාමාන්‍ය සීරුමාරුවේ දී විශද දෘෂ්ටියේ අවම දුරෙහි අතාත්වික ප්‍රතිබිම්බයක් සාදයි.
- (B) සංයුක්ත අණ්වීක්ෂයට අභිසාරි කාච දෙකක් ඇති අතර, අණ්වීක්ෂය සාමාන්‍ය සීරුමාරුවේ දී අතාත්වික විශාලිත ප්‍රතිබිම්බයක් අනන්තයේ සාදයි.
- (C) නක්ෂත්‍ර දුරේක්ෂයට අභිසාරී කාච දෙකක් ඇති අතර, දුරේක්ෂය සාමාන්‍ය සීරුමාරුවේ දී තාත්වික විශාලිත ප්‍රතිබිම්බයක් අනන්තයේ සාදයි.
ඉහත ප්‍රකාශවලින්,
රූපයේ පෙන්වා ඇති පරිදි $7.5\ \mathrm{cm}$ ක ඝනකමකින් යුත් පතුලක් සහිත සිලින්ඩරාකාර වීදුරු භාජනයක් $13.3\ \mathrm{cm}$ උ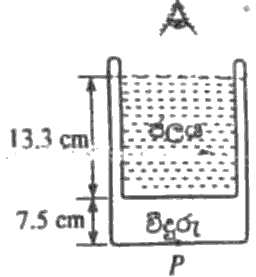
සකට ජලයෙන් පුරවා ඇත. වීදුරු සහ ජලයේ වර්තන අංක පිළිවෙළින් $1.5$ සහ $1.33$ වේ. ජල පෘෂ්ඨයට ඉහළින් නිරික්ෂණය කළ විට, භාජනයේ පතුලේ $P$ ලක්ෂ්‍යයෙහි පිහිටි සලකුණක දෘශ්‍ය ගැඹුර වන්නේ,
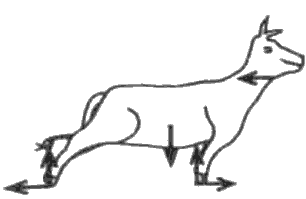
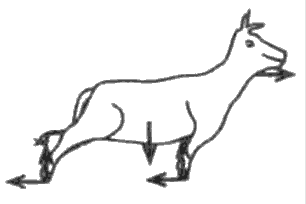
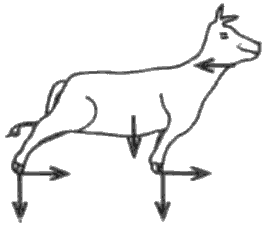
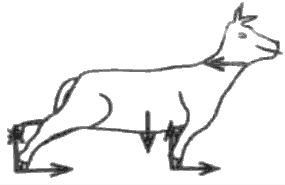
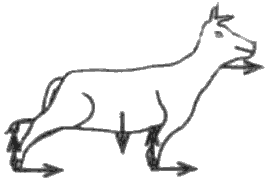
කඹයකින් ශක්තිමත් ගසක බැඳ ඇති ගවයෙක් යාබද ව ඇති පොල්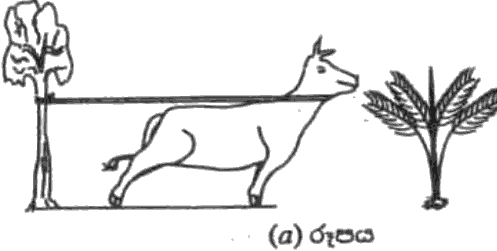
පැළයක් කෑමට උත්සාහ කරන ආකාරය $(a)$ රූපයෙහි පෙන්වා ඇත. ගවයා සඳහා නිදහස් වස්තු රූප සටහන (free-body diagram) නිවැරදි ව දැවෙන්නේ,
රූපයේ දක්වා ඇති කප්පි සැකසුම මගින්, $D$ ප්‍රකර්ෂණ උපකරණයකට සම්බන්ධ කර ඇති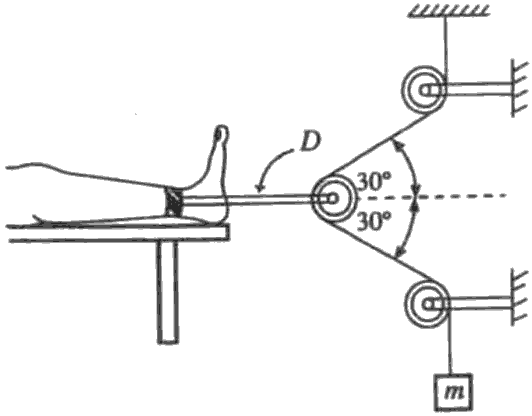 
රෝගියකුගේ පාදය මත බලයක් ඇති කරයි. කප්පි ඝර්ෂණයෙන් තොර වන අතර පද්ධතිය සමතුලිතතාවයේ පවතී. $D$ මගින් පාදය මත ක්‍රියාකරන තිරස් බලය $80\ \mathrm{N}$ නම්, එල්ලා ඇති $m$ ස්කන්ධයෙහි අගය වන්නේ $\Big( \cos 30^0 = \frac{\sqrt{3}}{2} \Big)$
එක එකෙහි ක්ෂේත්‍රඵලය $A$ වූ ලෝහ තහඩු දෙකක් භාවිත කර, පරතරය $0.9\ \mathrm{cm}$ සහිත වාතය මාධ්‍ය ලෙස ඇති $1\ \mathrm{F}$ සමාන්තර තහඩු ධාරිත්‍රකයක් සෑදුවහොත්, $A$ ක්ෂේත්‍රඵලයෙහි අගය ආසන්න වශයෙන් වන්නේ, ($\epsilon_0$ හි අගය $9 \times 10^{-12} \ \mathrm{Fm^{-1}}$ ලෙස ගන්න.)
දී ඇති පරිපථයෙහි බැටරියෙන්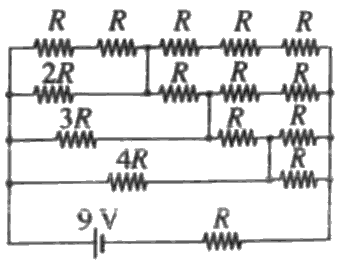
ඇදගන්නා ධාරාව (ඇම්පියරවලින්) වනුයේ,